题目内容
已知函数![]() .
.
(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点![]() (n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n,Sn)也在y=f′(x)的图象上;
(Ⅱ)求函数f(x)在区间(a-1,a)内的极值.
(Ⅰ)证明:因为![]() 所以
所以![]() ′(x)=x2+2x,
′(x)=x2+2x,
由点![]() 在函数y=f′(x)的图象上,得
在函数y=f′(x)的图象上,得![]() ,
,
即![]() ,又
,又![]() 所以
所以![]() ,
,
又因为![]() 1
1 ![]() ,所以数列
,所以数列![]() 是以3为首项,公差为2得等差数列。
是以3为首项,公差为2得等差数列。
所以![]() ,又因为
,又因为![]() ′(n)=n2+2n,所以
′(n)=n2+2n,所以![]() ,
,
故点![]() 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.
(Ⅱ)解:![]() ,
,
由![]() 得
得![]() .
.
当x变化时,![]()
![]() 的变化情况如下表:
的变化情况如下表:
| x | (-∞,-2) | -2 | (-2,0) | 0 | (0,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 极大值 | 极小值 |
注意到![]() ,从而
,从而
①当![]() ,此时
,此时![]() 无极小值;
无极小值;
②当![]() 的极小值为
的极小值为![]() ,此时
,此时![]() 无极大值;
无极大值;
③当![]() 既无极大值又无极小值.
既无极大值又无极小值.

练习册系列答案
相关题目
 .
. 的值域.
的值域.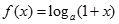 ,
,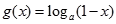 ,
,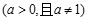 .
.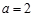 ,函数
,函数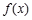 的定义域为
的定义域为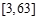 ,求函数
,求函数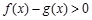 的
的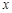 的取值范围.
的取值范围. 定义域为
定义域为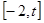 (
(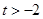 ),设
),设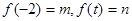 .
.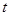 的取值范围,使得函数
的取值范围,使得函数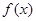 在
在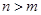 ;
;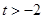 ,总存在
,总存在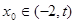 ,满足
,满足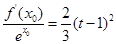 ,并确定这样的
,并确定这样的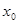 的个数.
的个数.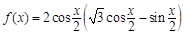 .
.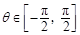 ,且
,且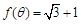 ,求
,求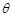 的值;
的值;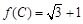 ,且△ABC的面积为
,且△ABC的面积为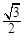 ,求sinA+sinB的值.
,求sinA+sinB的值. .
. 在
在 上单调递增,求
上单调递增,求 的取值范围。
的取值范围。 与
与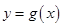 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求 轴的垂线分别与
轴的垂线分别与 的图像和
的图像和 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作 ,以T为切点作
,以T为切点作 .是否存在实数
.是否存在实数