题目内容
(本小题满分12分) 已知函数 .
.
(1) 设F(x)=
 在
在 上单调递增,求
上单调递增,求 的取值范围。
的取值范围。
(2)若函数 与
与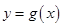 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求 的取值范围;
的取值范围;
(3)在(2)的条件下,过线段MN的中点作 轴的垂线分别与
轴的垂线分别与 的图像和
的图像和 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作 的切线
的切线 ,以T为切点作
,以T为切点作 的切线
的切线 .是否存在实数
.是否存在实数 使得
使得

 ,如果存在,求出
,如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】
 (2)由
(2)由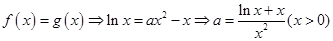
令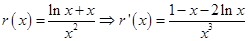
当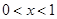 时,
时,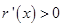 ,则
,则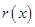 单调递增
单调递增
当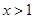 时,
时,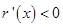 ,则
,则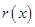 单调递减,且
单调递减,且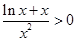
所以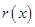 在
在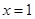 处取到最大值
处取到最大值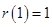 ,
,
所以要使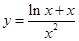 与
与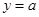 有两个不同的交点,则有
有两个不同的交点,则有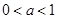 8分
8分
(2)不妨设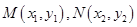 ,且
,且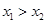 ,则
,则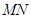 中点的坐标为
中点的坐标为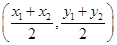
以S、T为切点的切线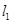 、
、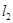 的斜率分别为
的斜率分别为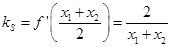

【解析】略

练习册系列答案
相关题目