Question

【题目】如图，倾斜角为a的直线经过抛物线的焦点F，且与抛物线交于A、B两点．

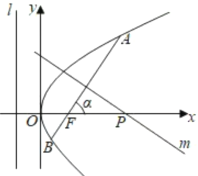
（1）求抛物线的焦点F的坐标及准线的方程；

（2）若a为锐角，作线段AB的垂直平分线m交x轴于点P，证明|FP|-|FP|cos2a为定值，并求此定值．

Answer 1

【答案】（1）（2）8

【解析】

试题（1）根据抛物线的标准方程，可求抛物线的焦点F的坐标及准线l的方程；（2）作AC⊥l，BD⊥l，垂足为C，D，求出|FA|，|FB|，即可得到结论

试题解析：（1）解：设抛物线的标准方程为，则，从而因此焦点的坐标为（2，0）．又准线方程的一般式为．从而所求准线l的方程为．

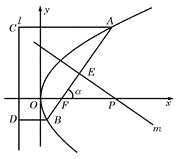
（2）解法一：如图（21）图作AC⊥l，BD⊥l，垂足为C、D，则由抛物线的定义知|FA|=|AC|,|FB|=|BD|．

记A的横坐标别为xx，则|FA|＝|AC|＝解得，

类似地有，解得．

记直线m与AB的交点为E，则

，

所以．故．

解法二：设，，直线AB的斜率为，则直线方程为．

将此式代入,得，故．

记直线m与AB的交点为，则

，，故直线m的方程为．

令y=0,得P的横坐标故．

从而为定值．