题目内容
【题目】设集合![]() 是集合
是集合![]() …,
…,![]() 的子集.记
的子集.记![]() 中所有元素的和为
中所有元素的和为![]() (规定:
(规定:![]() 为空集时,
为空集时,![]() =0).若
=0).若![]() 为3的整数倍,则称
为3的整数倍,则称![]() 为
为![]() 的“和谐子集”.
的“和谐子集”.
求:(1)集合![]() 的“和谐子集”的个数;
的“和谐子集”的个数;
(2)集合![]() 的“和谐子集”的个数.
的“和谐子集”的个数.
【答案】(1)![]() 的“和谐子集”的个数等于4.(2)
的“和谐子集”的个数等于4.(2)![]()
【解析】
(1)由集合的子集可得:集合A1的“和谐子集”为::,{3},![]() 共4个,
共4个,
(2)由即时定义的理解,分类讨论的数学思想方法可得:讨论集合An+1={1,2,3,……,3n﹣2,3n﹣1,3n,3n+1,3n+2,3n+3}中的“和谐子集”的情况,以新增元素3n+1,3n+2,3n+3为标准展开讨论即可得解
(1)集合![]() 的子集有:
的子集有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中所有元素和为3的整数倍的集合有:![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() 的“和谐子集”的个数等于4.
的“和谐子集”的个数等于4.
(2)记![]() 的“和谐子集”的个数等于
的“和谐子集”的个数等于![]() ,即
,即![]() 有
有![]() 个所有元素和为3的整数倍的子集;
个所有元素和为3的整数倍的子集;
另记![]() 有
有![]() 个所有元素和为3的整数倍余1的子集,有
个所有元素和为3的整数倍余1的子集,有![]() 个所有元素和为3的整数
个所有元素和为3的整数
倍余2的子集.
由(1)知,![]() .
.
集合 的“和谐子集”
的“和谐子集”
有以下四类(考查新增元素![]() ):
):
第一类 集合![]() …,
…,![]() 的“和谐子集”,共
的“和谐子集”,共![]() 个;
个;
第二类 仅含一个元素![]() 的“和谐子集”,共
的“和谐子集”,共![]() 个;
个;
同时含两个元素![]() 的“和谐子集”,共
的“和谐子集”,共![]() 个;
个;
同时含三个元素![]() 的“和谐子集”,共
的“和谐子集”,共![]() 个;
个;
第三类 仅含一个元素![]() 的“和谐子集”,共
的“和谐子集”,共![]() 个;
个;
同时含两个元素![]() 的“和谐子集”,共
的“和谐子集”,共![]() 个;
个;
第四类 仅含一个元素![]() 的“和谐子集”,共
的“和谐子集”,共![]() 个;
个;
同时含有两个元素![]() 的“和谐子集”,共
的“和谐子集”,共![]() 个,
个,
所以集合![]() 的“和谐子集”共有
的“和谐子集”共有![]() 个.
个.
同理得![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,
所以数列![]() 是以2为首项,公比为2 的等比数列.
是以2为首项,公比为2 的等比数列.
所以![]() .同理得
.同理得![]() .
.
又![]() ,所以
,所以![]() .
.

 作业辅导系列答案
作业辅导系列答案【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: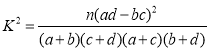 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%

