题目内容
某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
(1)求年推销金额y与工作年限x之间的相关系数;
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
(参考数据:
| 1.04 |
参考公式:
线性相关系数公式:
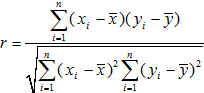
线性回归方程系数公式:
 |
| y |
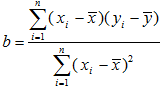 ,a=
,a=| y |
| x |
分析:(1)将表中数据,先求出x,y的平均数,累加相关的数据后,代入相关系数公式,即可求出推销金额y与工作年限x之间的相关系数(2)根据表中数据,计算出回归系数b,及a即可得到推销金额y关于工作年限x的线性回归方程
(3)根据(2)的结论,将工作年限为11年代,代入推销金额y关于工作年限x的线性回归方程,即可预报出他的年推销金额的估算值.
(3)根据(2)的结论,将工作年限为11年代,代入推销金额y关于工作年限x的线性回归方程,即可预报出他的年推销金额的估算值.
解答:解:(1)由
(xi-
)(yi-
)=10,
(xi-
)2=20,
(yi-
)2=5.2,
可得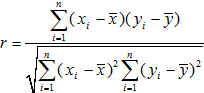 =
=
≈0.98.
即年推销金额y与工作年限x之间的相关系数约为0.98.
(2)由(1)知,r=0.98>0.959=r0.01,
∴可以认为年推销金额y与工作年限x之间具有较强的线性相关关系.
设所求的线性回归方程为
=bx+a,
则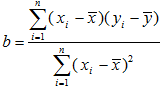 =
=
=0.5,a=
-b
=0.4.
∴年推销金额y关于工作年限x的线性回归方程为
=0.5x-0.4
(3)由(2)可知,当x=11时
=0.5x+0.4=0.5×11+0.4=5.9万元.
∴可以估计第6名推销员的年推销金额为5.9万元.
| n |
 |
| i=1 |
. |
| x |
. |
| y |
| n |
 |
| i=1 |
. |
| x |
| n |
 |
| i=1 |
. |
| y |
可得
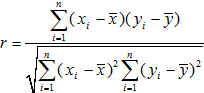 =
=| 10 | ||
|
即年推销金额y与工作年限x之间的相关系数约为0.98.
(2)由(1)知,r=0.98>0.959=r0.01,
∴可以认为年推销金额y与工作年限x之间具有较强的线性相关关系.
设所求的线性回归方程为
| ? |
| y |
则
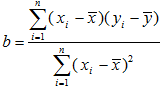 =
=| 10 |
| 20 |
| y |
| x |
∴年推销金额y关于工作年限x的线性回归方程为
| ? |
| y |
(3)由(2)可知,当x=11时
| ? |
| y |
∴可以估计第6名推销员的年推销金额为5.9万元.
点评:求回归直线的方程,关键是要求出回归直线方程的系数,由已知的变量x,y的值,我们计算出变量x,y的平均数,及xi,xiyi的累加值,代入回归直线系数公式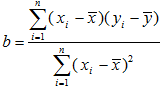 ,a=
,a=
-b
,即可求出回归直线的系数,进而求出回归直线方程.
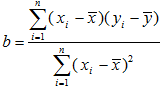 ,a=
,a=. |
| y |
. |
| x |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某电脑公司有6名产品推销员,其工作年限与年推销金额的数据如下表:
(1)以工作年限为自变量x,推销金额为因变量y,作出散点图;
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
(本小题满分15分)某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限 | 3 | 5 | 6 | 7 | 9 |
| 推销金额 | 2 | 3 | 3 | 4 | 5 |
(Ⅰ)求年推销金额![]() 与工作年限x之间的相关系数;(Ⅱ)求年推销金额
与工作年限x之间的相关系数;(Ⅱ)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.(参考数据:;由检验水平0.01及
的线性回归方程;(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.(参考数据:;由检验水平0.01及![]() ,查表得
,查表得![]() .)
.)
某电脑公司有6名产品推销员,其中5名产品推销员工作年限与年推销金额数据如下表:
|
推销员编号 |
1 |
2 |
3 |
4 |
5 |
|
工作年限 |
3 |
5 |
6 |
7 |
9 |
|
推销金额 |
2 |
3 |
3 |
4 |
5 |
(Ⅰ) 求年推销金额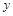 关于工作年限
关于工作年限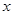 的线性回归方程
的线性回归方程
(Ⅱ)若第6名推销员的工作年限为11年,试估计他的年推销金额.
某电脑公司有6名产品推销员,其中5名推销员的工作年限与年推销金额数据如下表:
|
推销员编号 |
1 |
2 |
3 |
4 |
5 |
|
工作年限 |
3 |
5 |
6 |
7 |
9 |
|
年推销金额 |
2 |
3 |
3 |
4 |
5 |
(1)求年推销金额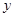 关于工作年限
关于工作年限 的线性回归方程.
的线性回归方程.
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
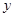 /万元
/万元