题目内容
(7分)已知圆C:
(1)若圆C被直线 截得的弦长为
截得的弦长为 ,求
,求 的值;
的值;
(2)求在(1)的条件下过点( )的切线方程;
)的切线方程;
(3)若圆C与直线 交于M、N两点,且OM⊥ON(O为坐标原点),求m的值。
交于M、N两点,且OM⊥ON(O为坐标原点),求m的值。
【答案】
解 :(1)由D2+E2-4F=4+16-4m=20-4m>0,得m<5。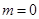 成立。
成立。
(2)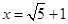 或
或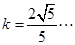 方程略
方程略
(3)(联立)设M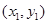 ,N
,N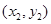 ,由OM⊥ON得x1x2+
y1y2=0。
,由OM⊥ON得x1x2+
y1y2=0。
将直线方程x+2y-4=0与曲线C:x2+y2-2x-4y+m=0联立并消去y得
5x2-8x+4m-16=0,由韦达定理得x1+x2=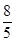 ①,x1x2=
①,x1x2=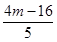 ②,又由x+2y-4=0得y=
②,又由x+2y-4=0得y=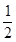 (4-x),
∴x1x2+y1y2=x1x2+
(4-x),
∴x1x2+y1y2=x1x2+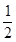 (4-x1)·
(4-x1)·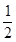 (4-x2)=
(4-x2)=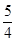 x1x2-( x1+x2)+4=0。将①、②代入得m=
x1x2-( x1+x2)+4=0。将①、②代入得m=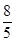 .
.
【解析】略

练习册系列答案
相关题目
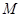 (1,3),与直线x+2y-7=0相切.
(1,3),与直线x+2y-7=0相切. 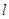 :
: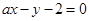
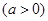 与圆C相交于A、B两点,求实数
与圆C相交于A、B两点,求实数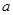 的取值范围;
的取值范围;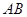 的垂直平分线过点
的垂直平分线过点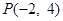 ,
若存在,求出实数
,
若存在,求出实数 :
:
 与圆C相交于A、B两点,求实数
与圆C相交于A、B两点,求实数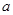 的取值范围;
的取值范围; 的垂直平分线
的垂直平分线 ,
若存在,求出实数
,
若存在,求出实数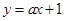 与双曲线C:
与双曲线C: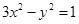 相交于A、B两点.
相交于A、B两点.