题目内容
已知函数f（x）=2x，|（x≥0），图象如图所示．函数g（x）=-x2-2x+a，（x＜0），其图象经过点A（-1，2）．（1）求实数a的值，并在所给直角坐标系xOy内做出函数g（x）的图象；
（2）设h（x）=
，根据h（x）的图象写出其单调区间．
【答案】分析：（1 ）由g（x）的图象经过点A（-1，2），代入可求a，进而可求g（x）
（2）结合函数的图象可求函数的单调区间
解答：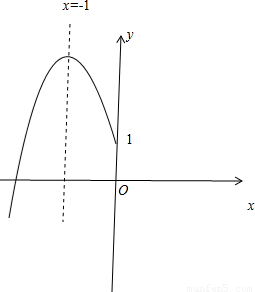
解：（1 ）因为g（x）的图象经过点A（-1，2），代入解得 a=1
∴g（x）=-x2-2x+1
（2 ） 函数h（x）
，结合函数的图象可知函数的单调增区间为（-∞，-1），（0，+∞）
函数h（x）的单调减区间为（-1，0）
点评：本题主要考查了函数值的求解，二次函数的图象的做法及利用函数的 图象给出函数的单调区间，属于基础试题
（2）结合函数的图象可求函数的单调区间
解答：
解：（1 ）因为g（x）的图象经过点A（-1，2），代入解得 a=1∴g（x）=-x2-2x+1
（2 ） 函数h（x）
，结合函数的图象可知函数的单调增区间为（-∞，-1），（0，+∞）函数h（x）的单调减区间为（-1，0）
点评：本题主要考查了函数值的求解，二次函数的图象的做法及利用函数的 图象给出函数的单调区间，属于基础试题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目