题目内容
已知函数 满足下述条件:对任意实数
满足下述条件:对任意实数 ,当
,当 时,总有
时,总有 ,则实数
,则实数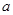 的取值范围是( )
的取值范围是( )
A.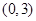 | B. | C. | D. |
D
解析试题分析:因为函数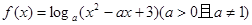 满足下述条件:对任意实数
满足下述条件:对任意实数 ,当
,当 时,总有
时,总有 ,所以函数在
,所以函数在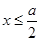 时是减函数,而t=
时是减函数,而t= 在
在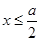 时 是减函数,所以a>1,且
时 是减函数,所以a>1,且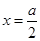 时,
时, =
=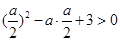 ,解得
,解得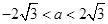 ,故实数
,故实数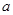 的取值范围是
的取值范围是 ,选D。
,选D。
考点:本题主要考查复合函数、对数函数的单调性。
点评:小综合题,复合函数的单调性判断依据:内外层函数“同增异减”。对于对数函数,要注意真数大于零。

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
下列函数中,是奇函数且在区间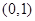 内单调递减的函数是( )
内单调递减的函数是( )
A.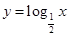 | B.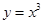 | C.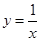 | D.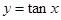 |
函数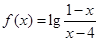 的定义域为( )
的定义域为( )
A.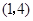 | B.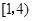 |
C.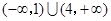 | D.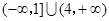 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D.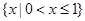 |
函数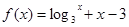 零点所在大致区间是( )
零点所在大致区间是( )
| A.(1,2) | B.(2,3) | C.(3,4) | D.(4,5) |
 ,若
,若 ,则
,则 =( )
=( )
A. | B. | C. | D. |
设 ,用二分法求方程
,用二分法求方程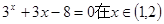 内近似解的过程
内近似解的过程
中得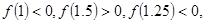 则方程的根落在区间
则方程的根落在区间
A.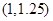 | B. | C.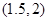 | D.不能确定 |
若函数 与函数
与函数 在区间
在区间 上都是减函数,则实数的取值范围为( )
上都是减函数,则实数的取值范围为( )
A. | B. | C. | D.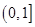 |
 时,在同一坐标系中,函数
时,在同一坐标系中,函数 与
与 的图象是
的图象是