Question

已知平面上两点A（3，-3）及B（2，15），在直线l：3x-4y+4=0上有一点P，可使||PB|-|PA||最大，则点P的坐标为

 

．

Answer 1

分析：作点A关于直线l的对称点C，作直线BC交l于P点，此时||PB|-|PA||最大，则点P为所求点．

解答：解：作点A关于直线l的对称点C，作直线BC交l于P点，此时||PB|-|PA||最大，则点P为所求点．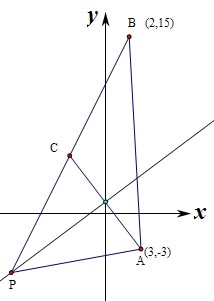
设C（a，b），
则满足AC⊥l，
∵直线3x-4y+4=0的斜率k=

3

4

，
则

-3-b 3-a • 3 4 =-1 3× a+3 2 -4× b-3 2 +4=0

，
即

4a+3b=3 3a-4b=-29

，
解得a=-3，b=5，即C（-3，5）．
此时直线BC的方程为

y-15

5-15

=

x-2

-3-2

，
即

y-15

-10

=

x-2

-5

，
∴y=2x+11，
由

y=2x+11 3x-4y+4=0

，
解得

x=-8 y=-5

，
即P（-8，-5），
故答案为：（-8，-5）．

点评：本题考查的是最短线路问题，解答此类题目的关键是根据轴对称的性质画出图形，再由两点之间线段最短的知识求解．