题目内容
已知平面上两点A(4,1)和B(3,3),在直线l:3x-y-1=0上找一点M,使|MA|+|MB|最小,求点M的坐标.
答案:
解析:

解析:
解:如图,作点B关于直线l的对称点C,设AC所在直线与直线l的交点为M,此时|MA|+|MB|取得最小值.

设点C的坐标为(x0,y0),因为线段BC被l垂直平分,
所以
解得x0=0,y0=4,即点C的坐标为(0,4).
由两点式易得,AC所在直线的方程为3x+4y-16=0.
与3x-y-1=0联立,解得x=![]() ,y=3.
,y=3.
所以点M的坐标为![]() .
.
点评:求两条线段的和的最小值,要与初中所学的对称知识紧密联系.求点关于直线l的对称点的问题,要用好两个条件:一是两对称点的中点在直线l上;二是两对称点的连线垂直于直线l.

练习册系列答案
相关题目
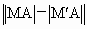 最大,求M的坐标及最大值
最大,求M的坐标及最大值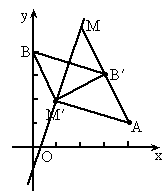
 最大,求M的坐标及最大值
最大,求M的坐标及最大值