题目内容
【题目】在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() ,且
,且![]() 为等边三角形,若四棱锥
为等边三角形,若四棱锥![]() 的体积与四棱锥
的体积与四棱锥![]() 外接球的表面积大小之比为
外接球的表面积大小之比为![]() ,则四棱锥
,则四棱锥![]() 的表面积为___________.
的表面积为___________.
【答案】![]()
【解析】
设四棱锥![]() 外接球的球心为
外接球的球心为![]() ,等边三角形
,等边三角形![]() 外接圆的圆心为
外接圆的圆心为![]() ,则
,则![]() 为
为![]() 的重心,可证四边形
的重心,可证四边形![]() 为矩形,所以
为矩形,所以![]() .设正方形
.设正方形![]() 的边长为
的边长为![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,得到四棱锥
,得到四棱锥![]() 外接球的表面积和体积为,结合题目条件解得
外接球的表面积和体积为,结合题目条件解得![]() ,求出四棱锥
,求出四棱锥![]() 的各个面的面积,从而求出四棱锥
的各个面的面积,从而求出四棱锥![]() 的表面积.
的表面积.
如图,
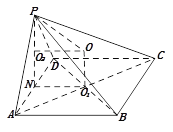
连接![]() ,
,![]() 交于点
交于点![]() ,取
,取![]() 的中点为
的中点为![]() ,连接
,连接![]() .
.
设四棱锥![]() 外接球的球心为
外接球的球心为![]() ,等边三角形
,等边三角形![]() 外接圆的圆心为
外接圆的圆心为![]() ,
,
则![]() 为
为![]() 的重心,则
的重心,则![]() ,正方形
,正方形![]() 外接圆的圆心为
外接圆的圆心为![]() .
.
因为![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以四边形![]() 为矩形,
为矩形,
所以![]() .
.
设正方形![]() 的边长为
的边长为![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,
,
所以四棱锥![]() 外接球的半径为
外接球的半径为![]() ,
,
所以四棱锥![]() 外接球的表面积为
外接球的表面积为![]() ,
,
四棱锥![]() 的体积为
的体积为![]() ,
,
所以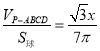 ,即
,即![]() ,解得
,解得![]() ,
,
所以正方形![]() 的边长为2,所以
的边长为2,所以![]() ,
,
所以四棱锥![]() 的表面积为
的表面积为![]() .
.
故答案为:![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目