题目内容
如图,已知圆心坐标为 的圆
的圆 与
与 轴及直线
轴及直线 均相切,切点分别为
均相切,切点分别为 、
、 ,另一圆
,另一圆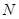 与圆
与圆 、
、 轴及直线
轴及直线 均相切,切点分别为
均相切,切点分别为 、
、 。
。
(1)求圆 和圆
和圆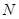 的方程;
的方程;
(2)过 点作
点作 的平行线
的平行线 ,求直线
,求直线 被圆
被圆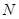 截得的弦的长度;
截得的弦的长度;

(1)圆 的方程为
的方程为 ,圆
,圆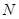 的方程为
的方程为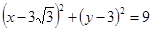
(2)
解析试题分析:(1)根据圆的圆心坐标和半径求圆的标准方程.(2)直线和圆相交,根据半径,弦长的一半,圆心距求弦长.(3)圆的弦长的常用求法:(1)几何法:求圆的半径 ,弦心距
,弦心距 ,弦长
,弦长 ,则
,则
(2)代数方法:运用根与系数的关系及弦长公式 .
.
试题解析:解(1)由于圆 与
与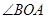 的两边相切,故
的两边相切,故 到
到 及
及 的距离均为圆
的距离均为圆 的半径,则
的半径,则 在
在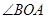 的角平分线上,同理,
的角平分线上,同理,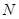 也在
也在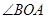 的角平分线上,
的角平分线上,
即 三点共线,且
三点共线,且 为
为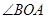 的角平分线,
的角平分线,
 的坐标为
的坐标为 ,
, 到
到 轴的距离为1,即:圆
轴的距离为1,即:圆 的半径为1,
的半径为1, 圆
圆 的方程为
的方程为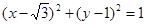 ; 3分
; 3分
设圆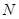 的半径为
的半径为 ,由
,由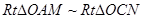 ,得:
,得: ,
,
即 ,
, ,
, 圆
圆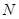 的方程为:
的方程为: ; 6分
; 6分
(2)由对称性可知,所求弦长等于过 点的
点的 的平行线被圆
的平行线被圆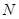 截得的弦长,
截得的弦长,
此弦所在直线方程为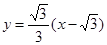 ,即
,即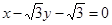 ,
,
圆心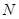 到该直线的距离
到该直线的距离 ,则弦长=
,则弦长= 3分
3分
考点:(1)圆的方程(2)直线和圆相交求弦长问题.(3)点到直线距离公式.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 ,直线
,直线 ,
, 上一点A的横坐标为
上一点A的横坐标为 ,过点A作圆M的两条切线
,过点A作圆M的两条切线 ,
, ,切点分别为B,C.
,切点分别为B,C.
 时,求直线
时,求直线 ?若存在,求出点A的坐标,若不存在,请说明理由.
?若存在,求出点A的坐标,若不存在,请说明理由. 与坐标轴交于点
与坐标轴交于点 .
. 垂直的圆的切线方程;
垂直的圆的切线方程; 是圆上任意一点(不在坐标轴上),直线
是圆上任意一点(不在坐标轴上),直线 交
交 轴于点
轴于点 ,直线
,直线 交直线
交直线 ,
, ,求弦
,求弦 为定值.
为定值.
 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在椭圆上,
在椭圆上, ,
, ,
, 的面积为
的面积为 .
. 轴上的圆,使圆在
轴上的圆,使圆在 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
 将圆
将圆 平分,且不经过第四象限,则
平分,且不经过第四象限,则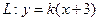 与圆
与圆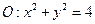 交于
交于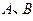 两点,则当
两点,则当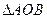 K*s^5#u的面积最大时,
K*s^5#u的面积最大时,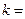 _______
_______ 与⊙
与⊙ 相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是 。
相交于A、B两点,且两圆在点A处的切线互相垂直,则线段AB的长度是 。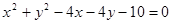 上至少有三个不同点到直线
上至少有三个不同点到直线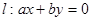 的距离为
的距离为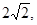 则直线
则直线 的斜率的取值区间为 .
的斜率的取值区间为 .