题目内容
(本小题满分12分)
已知直线![]() 所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到F的最小距离为2
所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到F的最小距离为2
(1)求椭圆C的标准方程;
(2)已知圆O:![]() ,直线
,直线![]() :
:![]() ,当点
,当点![]() 在椭圆C上运动时,直线
在椭圆C上运动时,直线![]() 与圆O是否相交于两个不同的点A,B?若相交,试求弦长|AB|的取值范围,否则说明理由.
与圆O是否相交于两个不同的点A,B?若相交,试求弦长|AB|的取值范围,否则说明理由.
(1)由已知得![]() ,所以F(3,0)-------------------------2分
,所以F(3,0)-------------------------2分
设椭圆方程C为![]() ,则
,则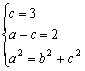 解得
解得![]() ---------4分
---------4分
所以椭圆方程为![]() --------------------------------------5分
--------------------------------------5分
(2)因为点![]() ,在椭圆C上运动,所以
,在椭圆C上运动,所以![]()
从而圆心O到直线![]() :
:![]() 的距离
的距离![]()
所以直线![]() 与圆O恒相交于两个不同的点A、B---------------------------------7分
与圆O恒相交于两个不同的点A、B---------------------------------7分
此时弦长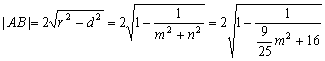 ---------------------------9分
---------------------------9分
由于![]() ,所以
,所以![]() ,则
,则![]() ---------------------12分
---------------------12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目