题目内容
(本小题满分12分)(注意:在试题卷上作答无效)
已知抛物线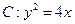 的焦点为F,过点
的焦点为F,过点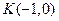 的直线
的直线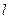 与
与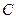 相交于
相交于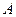 、
、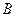 两点,点A关于
两点,点A关于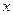 轴的对称点为D .
轴的对称点为D .
(Ⅰ)证明:点F在直线BD上;
(Ⅱ)设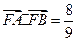 ,求
,求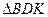 的内切圆M的方程 .
的内切圆M的方程 .
已知抛物线
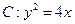 的焦点为F,过点
的焦点为F,过点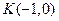 的直线
的直线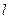 与
与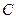 相交于
相交于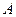 、
、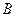 两点,点A关于
两点,点A关于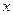 轴的对称点为D .
轴的对称点为D .(Ⅰ)证明:点F在直线BD上;
(Ⅱ)设
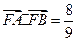 ,求
,求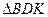 的内切圆M的方程 .
的内切圆M的方程 .(Ⅰ)证明见解析
(Ⅱ)
(Ⅱ)

本题主要考查抛物线方程、直线与抛物线的位置关系、对称性、圆的方程、平面向量的数量积,以及考查逻辑思维能力、运算能力、分析与解决问题的综合能力,同时考查方程的思想、数形结合的思想.
设 ,
, ,
, ,
,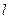 的方程为
的方程为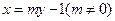 .
.
(Ⅰ)将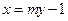 代人
代人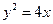 并整理得
并整理得
 ,
,
从而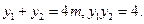
直线 的方程为
的方程为
 ,
,
即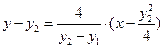
令
所以点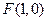 在直线
在直线 上
上
(Ⅱ)由①知,
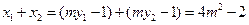

因为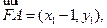
 ,
,

故 ,
,
解得
所以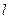 的方程为
的方程为
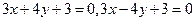
又由①知
故直线BD的斜率 ,
,
因而直线BD的方程为
因为KF为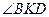 的平分线,故可设圆心
的平分线,故可设圆心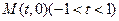 ,
,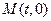 到
到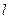 及BD的距离分别为
及BD的距离分别为 .
.
由 得
得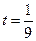 ,或
,或 (舍去),
(舍去),
故圆M的半径 .
.
所以圆M的方程为 .
.
设
 ,
, ,
, ,
,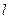 的方程为
的方程为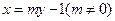 .
.(Ⅰ)将
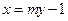 代人
代人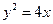 并整理得
并整理得 ,
,从而
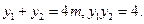
直线
 的方程为
的方程为 ,
,即
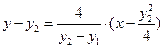
令

所以点
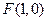 在直线
在直线 上
上(Ⅱ)由①知,
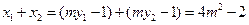

因为
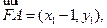
 ,
,
故
 ,
,解得

所以
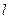 的方程为
的方程为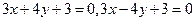
又由①知

故直线BD的斜率
 ,
,因而直线BD的方程为

因为KF为
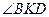 的平分线,故可设圆心
的平分线,故可设圆心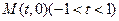 ,
,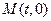 到
到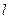 及BD的距离分别为
及BD的距离分别为 .
.由
 得
得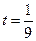 ,或
,或 (舍去),
(舍去),故圆M的半径
 .
.所以圆M的方程为
 .
.
练习册系列答案
相关题目
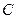 :
: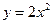 ,直线
,直线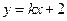 交
交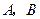 两点,
两点,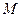 是线段
是线段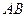 的中点,过
的中点,过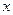 轴的垂线交
轴的垂线交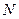 .
.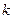 使
使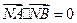 ,若存在,求
,若存在,求 = 。
= 。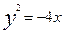 的焦点坐标是
的焦点坐标是 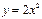 的焦点坐标是( )
的焦点坐标是( )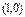
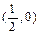


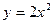 与直线
与直线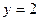 围成的封闭区域的面积为 .
围成的封闭区域的面积为 .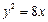 上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是
上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是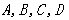 是抛物线
是抛物线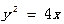 上四点,
上四点,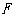 是焦点,且
是焦点,且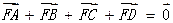 ,则
,则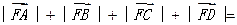 ( )
( )
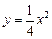 的焦点到直线
的焦点到直线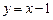 的距离为
的距离为


