题目内容
(09年江苏百校样本分析)(16分) 数列
![]()
(Ⅰ)求![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() 求
求![]() ;
;
(Ⅲ)设![]() ,
,![]() 为大于零的实数,
为大于零的实数,![]() 为数列{
为数列{![]() }的前n项和.是否存在实数λ,使得对任意正整数n,都有
}的前n项和.是否存在实数λ,使得对任意正整数n,都有![]()
![]()
![]() ? 若存在,求λ的取值范围;若不存在,说明理由.
? 若存在,求λ的取值范围;若不存在,说明理由.
解析:(Ⅰ) ![]()
![]() ………………2分
………………2分
一般地,![]()
即 ![]()
即数列![]() 是以
是以![]() 公差为2 的等差数列,
公差为2 的等差数列,
![]() ………………4分
………………4分
![]()
即数列![]() 是以
是以![]() 公比为
公比为![]() 的等比数列,
的等比数列,
![]()
综上可得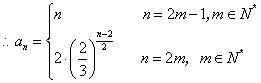 ………………6分
………………6分
(Ⅱ) ![]()
![]()
![]() ………………11分
………………11分
(Ⅲ)![]()
![]()
![]() ………………12分
………………12分
注意到对任意自然数n,![]() >0,
>0,
要对任意自然数n 及正数a, 都有![]()
![]()
![]() ,则必有
,则必有![]() , ………………13分
, ………………13分
此时,对任意自然数n ,![]()
![]() , ………………14分
, ………………14分
![]()
![]()
![]()
![]() 等价于
等价于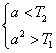 ,即
,即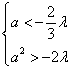 ,
, 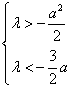 , ………………15分
, ………………15分
![]() 当
当![]() 时,存在实数
时,存在实数![]() ,使得对任意正整数n,都有
,使得对任意正整数n,都有![]()
![]()
![]() ;当
;当![]() 时不存在实数λ,使得对任意正整数n,都有
时不存在实数λ,使得对任意正整数n,都有![]()
![]()
![]() . ………………16分
. ………………16分

练习册系列答案
相关题目