��Ŀ����
 ��2010•���ն�ģ����ͼ��һ�鳤��������ABCD��AD=2��km����AB=1��km�����ڱ�AD���е�O������һ����ת����̽�յƣ�������ǡ�EOFʼ��Ϊ
��2010•���ն�ģ����ͼ��һ�鳤��������ABCD��AD=2��km����AB=1��km�����ڱ�AD���е�O������һ����ת����̽�յƣ�������ǡ�EOFʼ��Ϊ| �� |
| 4 |
| 3�� |
| 4 |
��1����0�ܦ���
| �� |
| 2 |
��2����0�ܦ���
| �� |
| 4 |
��3����̽�յ�ÿ9������ת��һ�����ء���OE��OAת��OC���ٻص�OA���ơ�һ�����ء�������OE��OA��OC������תʱ����ʱ�䣩����ת���Ľ��ٶȴ�Сһ������AB������һ��G���ҡ�AOG=
| �� |
| 6 |
��������1����O��OH��BC��HΪ���㣬���ۦ��ķ�Χ����0�ܦ���
ʱ��E�ڱ�AB�ϣ�F���߶�BH�ϣ�����S=S������OABH-S��OAE-S��OHF����
������
ʱ��E���߶�BH�ϣ�F���߶�CH�ϣ�S=S��OEF��
��2����0�ܦ���
ʱ�����û�������ʽ���S�����ֵ��ע��Ⱥų�����������
��3���ڡ�һ�����ء��У����OE��ת���ĽǶȣ����е�G���յ�ʱ����ת�ĽǶȣ��Ӷ��������һ�����ء��У���G���յ���ʱ�䣮
| �� |
| 4 |
| �� |
| 4 |
| �� |
| 2 |
��2����0�ܦ���
| �� |
| 4 |
��3���ڡ�һ�����ء��У����OE��ת���ĽǶȣ����е�G���յ�ʱ����ת�ĽǶȣ��Ӷ��������һ�����ء��У���G���յ���ʱ�䣮
���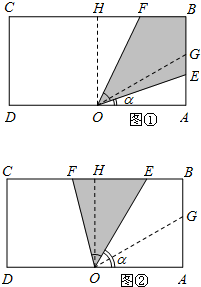 �⣺��1����O��OH��BC��HΪ���㣮
�⣺��1����O��OH��BC��HΪ���㣮
�ٵ�0�ܦ���
ʱ��
E�ڱ�AB�ϣ�F���߶�BH�ϣ���ͼ�٣���
��ʱ��AE=tan����FH=tan(
-��)������2�֣�
��S=S������OABH-S��OAE-S��OHF
=1-
tan��-
tan(
-��)�� ����4�֣�
�ڵ�
������
ʱ��
E���߶�BH�ϣ�F���߶�CH�ϣ���ͼ�ڣ���
��ʱ��EH=
��FH=
������6�֣�
��EF=
+
��
��S=S��OEF=
(
+
)��
����������S=
����8�֣�
��2����0�ܦ���
ʱ��S=1-
tan��-
tan(
-��)��
��S=2-
(1+tan��+
)�� ����10�֣�
��0�ܦ���
����0��tan����1����1��1+tan����2��
��1+tan��+
��2
��
��S��2-
��
��tan��=
-1ʱ��Sȡ�����ֵΪ2-
�� ����12�֣�
��3���ڡ�һ�����ء��У�OE��ת��2��
=
��
���е�G���յ�ʱ����ת��2��
=
�� ����14�֣�
��һ�����ء��У���G���յ���ʱ��Ϊ9��
=2�����ӣ�������16�֣�
 �⣺��1����O��OH��BC��HΪ���㣮
�⣺��1����O��OH��BC��HΪ���㣮�ٵ�0�ܦ���
| �� |
| 4 |
E�ڱ�AB�ϣ�F���߶�BH�ϣ���ͼ�٣���
��ʱ��AE=tan����FH=tan(
| �� |
| 4 |
��S=S������OABH-S��OAE-S��OHF
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| �� |
| 4 |
�ڵ�
| �� |
| 4 |
| �� |
| 2 |
E���߶�BH�ϣ�F���߶�CH�ϣ���ͼ�ڣ���
��ʱ��EH=
| 1 |
| tan�� |
| 1 | ||
tan(
|
��EF=
| 1 |
| tan�� |
| 1 | ||
tan(
|
��S=S��OEF=
| 1 |
| 2 |
| 1 |
| tan�� |
| 1 | ||
tan(
|
����������S=
|
��2����0�ܦ���
| �� |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| �� |
| 4 |
��S=2-
| 1 |
| 2 |
| 2 |
| 1+tan�� |
��0�ܦ���
| �� |
| 4 |
��1+tan��+
| 2 |
| 1+tan�� |
| 2 |
��S��2-
| 2 |
��tan��=
| 2 |
| 2 |
��3���ڡ�һ�����ء��У�OE��ת��2��
| 3�� |
| 4 |
| 3�� |
| 2 |
���е�G���յ�ʱ����ת��2��
| �� |
| 6 |
| �� |
| 3 |
��һ�����ء��У���G���յ���ʱ��Ϊ9��
| ||
|
������������Ҫ�����˽���������ʵ�������е�Ӧ�ã�ͬʱ���������û�������ʽ����ֵ���⣬�����е��⣮

��ϰ��ϵ�д�
�����Ŀ
 ��2010•���ն�ģ���ڵ�����ABC�У���֪AB=AC��B��-1��0����D��2��0��ΪAC���е㣮
��2010•���ն�ģ���ڵ�����ABC�У���֪AB=AC��B��-1��0����D��2��0��ΪAC���е㣮