题目内容
 (2010•江苏二模)在等腰△ABC中,已知AB=AC,B(-1,0),D(2,0)为AC的中点.
(2010•江苏二模)在等腰△ABC中,已知AB=AC,B(-1,0),D(2,0)为AC的中点.(1)求点C的轨迹方程;
(2)已知直线l:x+y-4=0,求边BC在直线l上的投影EF长的最大值.
分析:(1)设出C,进而可表示出D和A,进而利用B的坐标和AB=AC利用两点间的距离公式求得x和y的关系,进而根据A,B,C三点不共线判断出y≠0,则C点的轨迹方程可得.
(2)根据题意可求得BE的方程,设出直线CF的方程,当EF取得最大值时,直线CF与圆(x-1)2+y2=4相切.利用点到直线的距离求得b,则直线CF的方程可得.进而根据EF长的最大值是点B到CF的距离,答案可得.
(2)根据题意可求得BE的方程,设出直线CF的方程,当EF取得最大值时,直线CF与圆(x-1)2+y2=4相切.利用点到直线的距离求得b,则直线CF的方程可得.进而根据EF长的最大值是点B到CF的距离,答案可得.
解答: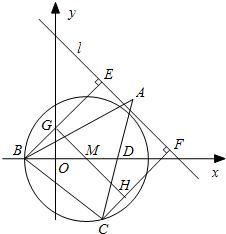 解:(1)设C(x,y),
解:(1)设C(x,y),
∵D(2,0)为AC的中点,
∴A(4-x,-y).
∵B(-1,0),由AB=AC,得AB2=AC2.
∴(x-5)2+y2=(2x-4)2+(2y)2.
整理,得(x-1)2+y2=4.
∵A,B,C三点不共线,∴y≠0.
则点C的轨迹方程为(x-1)2+y2=4(y≠0).
(2)由条件,易得
BE:x-y+1=0.
设CF:x-y+b=0,
当EF取得最大值时,
直线CF与圆(x-1)2+y2=4相切.
设M(1,0),由
=2,得b=2
-1(舍去),或b=-2
-1.
∴CF:x-y-2
-1=0.
∴EFmax等于点B到CF的距离
=
=
+2.
 解:(1)设C(x,y),
解:(1)设C(x,y),∵D(2,0)为AC的中点,
∴A(4-x,-y).
∵B(-1,0),由AB=AC,得AB2=AC2.
∴(x-5)2+y2=(2x-4)2+(2y)2.
整理,得(x-1)2+y2=4.
∵A,B,C三点不共线,∴y≠0.
则点C的轨迹方程为(x-1)2+y2=4(y≠0).
(2)由条件,易得
BE:x-y+1=0.
设CF:x-y+b=0,
当EF取得最大值时,
直线CF与圆(x-1)2+y2=4相切.
设M(1,0),由
| |1-0+b| | ||
|
| 2 |
| 2 |
∴CF:x-y-2
| 2 |
∴EFmax等于点B到CF的距离
=
|-1-0-2
| ||
|
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生运用解析几何的知识解决问题的能力.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 (2010•江苏二模)如图是一块长方形区域ABCD,AD=2(km),AB=1(km).在边AD的中点O处,有一个可转动的探照灯,其照射角∠EOF始终为
(2010•江苏二模)如图是一块长方形区域ABCD,AD=2(km),AB=1(km).在边AD的中点O处,有一个可转动的探照灯,其照射角∠EOF始终为