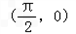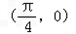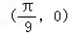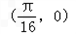题目内容
将函数
的图象上各点的横坐标伸长到原来的2倍，再向左平移
个单位，得到的函数图象的一条对称轴方程是（ ）A．
B．
C．
D．
【答案】分析：按照伸缩变换与平移变换的原则，直接求出变换后的函数的解析式，即可求出函数的对称轴方程．
解答：解：将函数
的图象上各点的横坐标伸长到原来的2倍，得到函数
，再向左平移
个单位，得到的函数
=sin（2x+
）的图象，函数的对称轴方程为：2x+
=kπ+
，k∈Z，
x=
，k∈Z，
当k=0时，
，
故选A．
点评：本题是基础题，考查三角函数的化简对称轴方程的求法，考查计算能力．
解答：解：将函数
的图象上各点的横坐标伸长到原来的2倍，得到函数，再向左平移个单位，得到的函数=sin（2x+）的图象，函数的对称轴方程为：2x+=kπ+，k∈Z，x=
，k∈Z，当k=0时，
，故选A．
点评：本题是基础题，考查三角函数的化简对称轴方程的求法，考查计算能力．
练习册系列答案
单元期中期末卷系列答案
相关题目
的图象上各点的横坐标长到原来的3倍，纵坐标不变，再把所得函数图象向右平行移动
个单位长度，得到的函数图象的一个对称中心是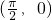
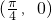
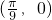
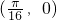
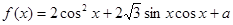，且当
时，
的最小值为2.（1）求
的值，并求
的图象上各点的纵坐标保持不变，横坐标缩短到原来的
倍，再把所得图象向右平移
个单位，得到函数
，求方程
在区间
上的所有根之和. 
，且当
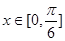时，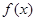
的最小值为2.
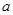的值，并求
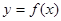的图象上各点的纵坐标保持不变，横坐标缩短到原来的
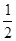倍，再把所得图象向右平移
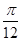个单位，得到函数
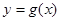，求方程
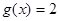在区间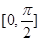
上的所有根之和.
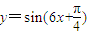的图象上各点的横坐标伸长到原来的3倍，再向右平移
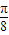个单位，得到的函数的一个对称中心（ ）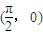
）
）
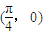
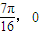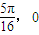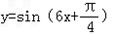的图象上各点的横坐标长到原来的3倍，纵坐标不变，再把所得函数图象向右平行移动
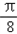个单位长度，得到的函数图象的一个对称中心是
