题目内容
已知椭圆C的中心为原点O,点F(1,0)是它的一个焦点,直线l过点F与椭圆C交于A,B两点,当直线l垂直于x轴时,
•
=
(I)求椭圆C的方程;
(II)已知点P为椭圆的上顶点,且存在实数t使
+
=t
成立,求实数t的值和直线l的方程.
| OA |
| OB |
| 1 |
| 2 |
(I)求椭圆C的方程;
(II)已知点P为椭圆的上顶点,且存在实数t使
| PA |
| PB |
| PF |
分析:(I)设椭圆C的方程为
+
=1(a>b>0),则a2-b2=1,当l垂直于x轴时,A,B两点的坐标分别是(1,
)和(1,-
),由
•
=(1,
)•(1,-
)=1-
,知a2=2b4,由此能求出椭圆C的方程.
(II)当直线斜率不存在时,A(1,
),B(1,-
),P(0,1),
=(1,
-1),
=(1,-
-1),
=(1,-1),由t使
+
=t
,得直线l的方程为x=1当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2),
=(x1,y1-1),
=(x2,y2-1),
=(1,-1),由t使
+
=t
,得直线l的方程为y=-x+1.由此能求出结果.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| b2 |
| a |
| OA |
| OB |
| b2 |
| a |
| b2 |
| a |
| b4 |
| a2 |
(II)当直线斜率不存在时,A(1,
| ||
| 2 |
| ||
| 2 |
| PA |
| ||
| 2 |
| PB |
| ||
| 2 |
| PF |
| PA |
| PB |
| PF |
| PA |
| PB |
| PF |
| PA |
| PB |
| PF |
解答:解:(I)设椭圆C的方程为
+
=1(a>b>0),
则a2-b2=1,①
∵当l垂直于x轴时,A,B两点的坐标分别是(1,
)和(1,-
),
∴
•
=(1,
)•(1,-
)=1-
,
则1-
=
,即a2=2b4.②
由①,②消去a,得2b4-b2-1=0.∴b2=1或b2=-
.
当b2=1时,a2=2.因此,椭圆C的方程为
+y2=1.
(II)当直线斜率不存在时,A(1,
),B(1,-
),P(0,1),
所以
=(1,
-1),
=(1,-
-1),
=(1,-1),
由t使
+
=t
,得t=2,直线l的方程为x=1
当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2),
所以,
=(x1,y1-1),
=(x2,y2-1),
=(1,-1),
由t使
+
=t
,得
,即
,
因为y1=k(x1-1),y2=k(x2-1),
所以,y1+y2=k(x1+x2-2),解得:k=-1
此时,直线l的方程为y=-x+1,
联立
,得3x2-4x=0,t=x1+x2=
,
∴当直线斜率存在时,t=
,直线l的方程为y=-x+1,
综上所述,存在实数t,且t=2时,直线方程x=1,
当t=1时,直线l的方程为y=-x+1.
| x2 |
| a2 |
| y2 |
| b2 |
则a2-b2=1,①
∵当l垂直于x轴时,A,B两点的坐标分别是(1,
| b2 |
| a |
| b2 |
| a |
∴
| OA |
| OB |
| b2 |
| a |
| b2 |
| a |
| b4 |
| a2 |
则1-
| b4 |
| a2 |
| 1 |
| 2 |
由①,②消去a,得2b4-b2-1=0.∴b2=1或b2=-
| 1 |
| 2 |
当b2=1时,a2=2.因此,椭圆C的方程为
| x2 |
| 2 |
(II)当直线斜率不存在时,A(1,
| ||
| 2 |
| ||
| 2 |
所以
| PA |
| ||
| 2 |
| PB |
| ||
| 2 |
| PF |
由t使
| PA |
| PB |
| PF |
当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2),
所以,
| PA |
| PB |
| PF |
由t使
| PA |
| PB |
| PF |
|
|
因为y1=k(x1-1),y2=k(x2-1),
所以,y1+y2=k(x1+x2-2),解得:k=-1
此时,直线l的方程为y=-x+1,
联立
|
| 4 |
| 3 |
∴当直线斜率存在时,t=
| 4 |
| 3 |
综上所述,存在实数t,且t=2时,直线方程x=1,
当t=1时,直线l的方程为y=-x+1.
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意分类讨论思想和等价转化思想的合理运用.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
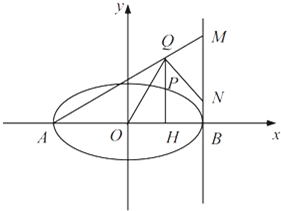 (2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
(2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为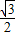 ,且点
,且点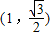 在该椭圆上.
在该椭圆上.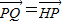 ,直线AQ与过点B 且垂直于x 轴的直线交于点M,
,直线AQ与过点B 且垂直于x 轴的直线交于点M,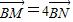 .求证:∠OQN为锐角.
.求证:∠OQN为锐角.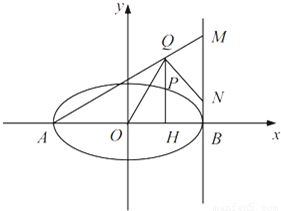
 =
=
 成立,求实数t的值和直线l的方程.
成立,求实数t的值和直线l的方程.