题目内容
 (2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
(2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
| ||
| 2 |
| ||
| 2 |
(1)求椭圆C的方程;
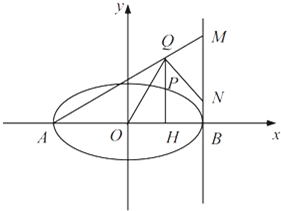
(2)如图,椭圆C 的长轴为AB,设 P 是椭圆上异于 A、B 的任意一点,PH⊥x轴,H为垂足,点Q 满足
| PQ |
| HP |
| BM |
| BN |
分析:(1)利用椭圆的离心率e=
=
,及点(1,
)在该椭圆上满足椭圆的方程与a2=b2+c2即可求出;
(2)设P(x0,y0)(-2<x0<2),由A(-2,0),PQ=HP,得到Q(x0,2y0),进而得到直线AQ的方程为y=
(x+2).令x=4即可得到点M的坐标;再根据向量共线
=4
即可得到点N的坐标,只要证明
•
>0且三点O,Q,N不共线即可得到∠OQN为锐角.
| c |
| a |
| ||
| 2 |
| ||
| 2 |
(2)设P(x0,y0)(-2<x0<2),由A(-2,0),PQ=HP,得到Q(x0,2y0),进而得到直线AQ的方程为y=
| 2y0 |
| x0+2 |
| BM |
| BN |
| QO |
| QN |
解答:解:(1)设椭圆C的方程为
+
=1,(a>b>0),
由题意可得 e=
=
,
又a2=b2+c2,∴4b2=a2.
∵椭圆C经过(1,
),代入椭圆方程有
+
=1,
解得b2=1.∴a2=4,
故椭圆C的方程为
+y2=1.
(2)设P(x0,y0)(-2<x0<2),
∵A(-2,0),
∵PQ=HP,∴Q(x0,2y0),
∴直线AQ的方程为y=
(x+2).
令x=2,得M(2,
).
∵B(2,0),
=4
,
∴N(2,
).
∴
=(-x0,-2y0),
=(2-x0,
).
∴
•
=-x0(2-x0)+(-2y0)•
=x0(x0-2)+
∵
+y02=1,
∴4y02=4-
∴
•
=2-x0.
∵-2<x0<2,
∴
•
=2-x0>0.
又O、Q、N不在同一条直线,
∴∠OQN为锐角.
| x2 |
| a2 |
| y2 |
| b2 |
由题意可得 e=
| c |
| a |
| ||
| 2 |
又a2=b2+c2,∴4b2=a2.
∵椭圆C经过(1,
| ||
| 2 |
| 1 |
| 4b2 |
| ||
| b2 |
解得b2=1.∴a2=4,
故椭圆C的方程为
| x2 |
| 4 |
(2)设P(x0,y0)(-2<x0<2),
∵A(-2,0),
∵PQ=HP,∴Q(x0,2y0),
∴直线AQ的方程为y=
| 2y0 |
| x0+2 |
令x=2,得M(2,
| 8y0 |
| x0+2 |
∵B(2,0),
| BM |
| BN |
∴N(2,
| y0 |
| x0+2 |
∴
| QO |
| QN |
| -2y0(1+x0) |
| x0+2 |
∴
| QO |
| QN |
| -2y0(1+x0) |
| x0+2 |
| 4y02(1+x0) |
| x0+2 |
∵
| x02 |
| 4 |
∴4y02=4-
| x | 2 0 |
∴
| QO |
| QN |
∵-2<x0<2,
∴
| QO |
| QN |
又O、Q、N不在同一条直线,
∴∠OQN为锐角.
点评:本题主要考查椭圆的方程与性质、向量相等于共线及夹角等基础知识,考查运算能力、推理论证以及分析问题、解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目