题目内容
已知双曲线 的左右焦点分别为
的左右焦点分别为 ,
, 为双曲线的离心率,P是双曲线右支上的点,
为双曲线的离心率,P是双曲线右支上的点, 的内切圆的圆心为I,过
的内切圆的圆心为I,过 作直线PI的垂线,垂足为B,则OB=
作直线PI的垂线,垂足为B,则OB=
| A.a | B.b | C.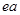 | D. |
A
解析试题分析:根据题意,利用切线长定理,再利用双曲线的定义,把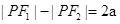 ,转化为
,转化为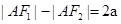 ,从而求得点H的横坐标.再在三角形PCF2中,由题意得,它是一个等腰三角形,从而在三角形
,从而求得点H的横坐标.再在三角形PCF2中,由题意得,它是一个等腰三角形,从而在三角形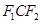 中,利用中位线定理得出OB,从而解决问题.
中,利用中位线定理得出OB,从而解决问题.
解:由题意知: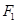 (-c,0)、
(-c,0)、 (c,0),内切圆与x轴的切点是点A,作图
(c,0),内切圆与x轴的切点是点A,作图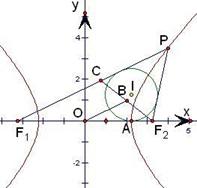
∵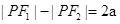 ,及圆的切线长定理知,
,及圆的切线长定理知,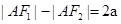 ,设内切圆的圆心横坐标为x,
,设内切圆的圆心横坐标为x,
则|(x+c)-(x-c)|=2a,∴x=a,在三角形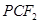 中,由题意得,它是一个等腰三角形,PC=PF2,
中,由题意得,它是一个等腰三角形,PC=PF2,
∴在三角形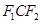 中,有:OB=
中,有:OB=
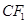 =
= (
(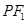 -PC)=
-PC)= (
(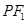 -
-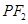 )=
)= ×2a=a.故选A.
×2a=a.故选A.
考点:双曲线的定义、切线长定理
点评:本题考查双曲线的定义、切线长定理.解答的关键是充分利用三角形内心的性质.属于基础题。

练习册系列答案
相关题目
设抛物线顶点在坐标原点,,准线方程为 ,则抛物线方程是( )
,则抛物线方程是( )
A. | B. | C. | D. |
椭圆 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
已知△ABC的周长为20,且顶点B(0,-4),C(0,4),则顶点A的轨迹方程是
A. (x≠0) (x≠0) | B. (x≠0) (x≠0) |
C. (x≠0) (x≠0) | D. (x≠0) (x≠0) |
已知 <4,则曲线
<4,则曲线 和
和 有( )
有( )
| A.相同的准线 | B.相同的焦点 | C.相同的离心率 | D.相同的长轴 |
椭圆 的焦距为( )
的焦距为( )
| A. 10 | B. 5 | C. | D. |
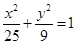 ,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设
,过椭圆右焦点F的直线L交椭圆于A、B两点,交y轴于P点。设 ,则
,则 等于( )
等于( ) B.
B.  C.
C.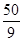 D.
D. 
 的焦点相同,则双曲线C的标准方程是( )
的焦点相同,则双曲线C的标准方程是( )



 的右焦点作倾斜角为
的右焦点作倾斜角为 的直线
的直线 ,交椭圆于A、B两点,O为坐标原点,则
,交椭圆于A、B两点,O为坐标原点,则 ( )
( ) C . -3或
C . -3或