题目内容

在数列{an}中，a1＝1，＝＋．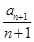

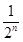(1)设bn＝，求数列{bn}的通项公式；

(2)求数列{an}的前n项和Sn．

 

【答案】

(1) bn＝2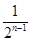－ (2) n(n＋1)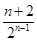＋－4

【解析】(1)由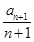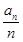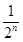＝＋可知bn＋1＝bn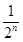＋,然后可利用叠加法求bn.

(2)再利用bn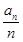＝可求出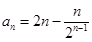,然后再利用分组求和和错位相减法求和即可．

解：(1)由已知得b1＝a1＝1且＝＋，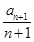

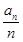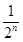即bn＋1＝bn＋，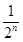

从而b2＝b1＋，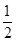

b3＝b2＋，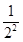

…

bn＝bn－1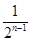＋ ( n≥2)，

于是bn＝b1＋＋＋…＋，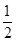

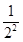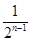＝2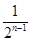－ ( n≥2)，      ………………4分

又b1＝1，       ………………5分

∴{bn}的通项公式bn＝2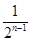－    .………………6分

(2)由(1)知an＝n·bn＝2n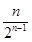－，     ………………7分

令Tn＝＋＋＋…＋，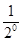

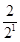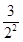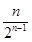则2Tn＝2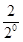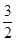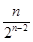＋＋＋…＋，    ………………8分

作差得：

Tn＝2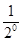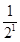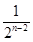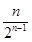＋(＋＋…＋)－＝4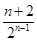－，     ………………10分

∴Sn＝(2＋4＋6＋…＋2n)－Tn

＝n(n＋1)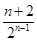＋－4. ………………12分

说明：各题如有其它解法可参照给分．

 

练习册系列答案
相关题目
在数列{an}中，
a
 
1
=1，an=
1
2
an-1+1（n≥2），则数列{an}的通项公式为an=
2-21-n
2-21-n
．
在数列{an}中，a 1=
1
3
，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=
1
an
（n∈N*）．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{
an
n
}的前n项和为Tn，证明：
1
3
≤Tn＜
3
4
．
在数列{an}中，a=
12
，前n项和Sn=n2an，求an+1．
在数列{an}中,a1=a,前n项和Sn构成公比为q的等比数列,________________.

(先在横线上填上一个结论,然后再解答)

在数列{an}中，a，并且对任意n∈N*，n≥2都有an•an-1=an-1-an成立，令bn=（n∈N*）．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设数列{}的前n项和为Tn，证明：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网