题目内容
(本小题12分)
如图所示,直三棱柱ABC—A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求 的长;
的长;
(2)求cos<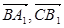 >的值;
>的值;
] (3)求证:A1B⊥C1M.
【答案】
如图,建立空间直角坐标系O—xyz.
(1)依题意得B(0,1,0)、N(1,0,1)
∴|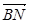 |=
|=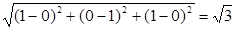 .
.
(2)依题意得A1(1,0,2)、B(0,1,0)、C(0,0,0)、B1(0,1,2)
∴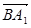 ={-1,-1,2},
={-1,-1,2},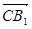 ={0,1,2,}
={0,1,2,}
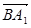 ·
·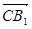 =3,|
=3,|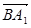 |=
|=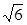 ,|
,|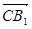 |=
|=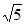
∴cos<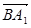 ,
,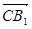 >=
>=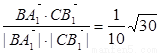 .
.
(3)证明:依题意,得C1(0,0,2)、M(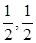 ,2),
,2),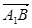 ={-1,1,2},
={-1,1,2},
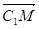 ={
={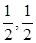 ,0}.∴
,0}.∴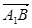 ·
·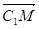 =-
=-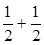 +0=0,
+0=0,
∴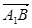 ⊥
⊥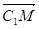 ,∴A1B⊥C1M.
,∴A1B⊥C1M.
【解析】略

练习册系列答案
相关题目

 是以原点
是以原点 为中心,以
为中心,以 、
、 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线 是以
是以 是曲线
是曲线 为钝角,若
为钝角,若 ,
, .
. 、
、 、
、 、
、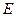 四点(如图),若
四点(如图),若 为
为 的中点,
的中点, 为
为 的中点,问
的中点,问 是否为定值?若是,求出定值;若不是,请说明理由.
是否为定值?若是,求出定值;若不是,请说明理由. <
< <
< <…<
<…< )是曲线C
)是曲线C
 上的n个点,点
上的n个点,点 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿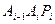 是正三角形(
是正三角形( 是坐标原点)。
是坐标原点)。

 的横坐标
的横坐标 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明 中,
中,
 ,
, 为
为 中点,若规定主视方向为垂直于平面
中点,若规定主视方向为垂直于平面 的方向,则可求得三棱柱左视图的面积为
的方向,则可求得三棱柱左视图的面积为 ;
;
 ;
; 的体积。
的体积。 海里的两个观测点。现位于B点正北方向、A点北偏东
海里的两个观测点。现位于B点正北方向、A点北偏东 方向的C点有一艘轮船发出求救信号,位于B点北偏西
方向的C点有一艘轮船发出求救信号,位于B点北偏西 、A点北偏西
、A点北偏西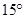 的D点的救援船立即前往营救,其航行速度为
的D点的救援船立即前往营救,其航行速度为 海里/小时.问该救援船到达C点需要多少时间?
海里/小时.问该救援船到达C点需要多少时间?
 的算法的
的算法的