题目内容
(本小题满分12分)
已知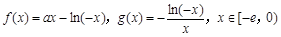 .
.
(1)讨论a = – 1时,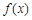 的单调性、极值;
的单调性、极值;
(2)求证:在(1)的条件下,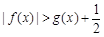 ;
;
(3)是否存在实数a,使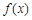 的最小值是3,如果存在,求出a的值;若不存在,
的最小值是3,如果存在,求出a的值;若不存在,
请说明理由.
【答案】
解:(1) ∵ 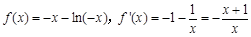
∴ 当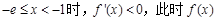 单调递减
单调递减
当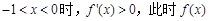 单调递增
单调递增
∴  w.w.w.zxxk.c.o.m
w.w.w.zxxk.c.o.m
(2) ∵  上的最小值为1,
上的最小值为1,
∴ 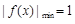
令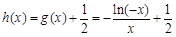
又∵ 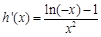
∴ 当
∴ 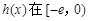 上单调递减w.w.w.k.
s.5.u.c.o.m
上单调递减w.w.w.k.
s.5.u.c.o.m
∴ 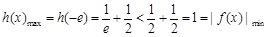
∴ 当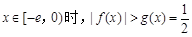
(3) 假设存在实数a,使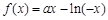 有最小值3,
有最小值3,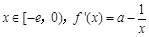
①当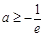 时,由于
时,由于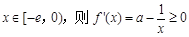
∴ 函数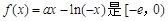 上的增函数,
上的增函数,
∴ 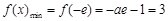 ,
,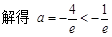 (舍去)
(舍去)
②当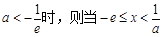 时,
时, ,此时
,此时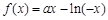 是增函数
是增函数
当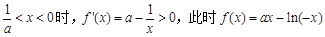 是增函数
是增函数
∴ 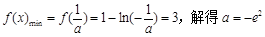
由①、②知,存在实数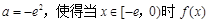 有最小值3。
有最小值3。
【解析】略

练习册系列答案
相关题目