题目内容
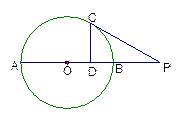
如图,已知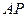 是⊙O的切线,
是⊙O的切线,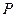 为切点,
为切点,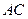 是⊙O的割线,与⊙O交于
是⊙O的割线,与⊙O交于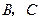 两点,圆心
两点,圆心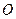 在
在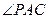 的内部,点
的内部,点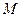 是
是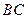 的中点.
的中点.
(Ⅰ)证明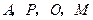 四点共圆;
四点共圆;
(Ⅱ)求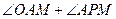 的大小.
的大小.
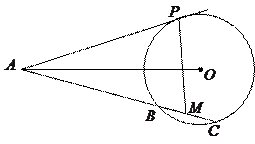
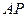 是⊙O的切线,
是⊙O的切线,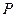 为切点,
为切点,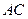 是⊙O的割线,与⊙O交于
是⊙O的割线,与⊙O交于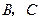 两点,圆心
两点,圆心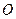 在
在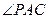 的内部,点
的内部,点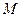 是
是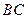 的中点.
的中点.(Ⅰ)证明
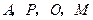 四点共圆;
四点共圆;(Ⅱ)求
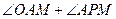 的大小.
的大小.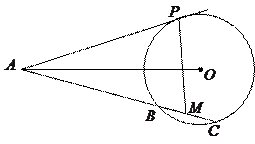
(Ⅰ)证明:连结 .
.
因为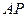 与⊙O相切于点
与⊙O相切于点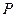 ,所以
,所以 . (1分)
. (1分)
因为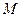 是⊙O的弦
是⊙O的弦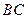 的中点,所以
的中点,所以 . (2分)
. (2分)
于是 . (3分)
. (3分)
由圆心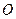 在
在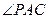 的内部,可知四边形
的内部,可知四边形 的对角互补,所以
的对角互补,所以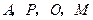 四点共圆.(5分)
四点共圆.(5分)
(Ⅱ)解:由(Ⅰ)得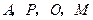 四点共圆,所以
四点共圆,所以 .(7分)
.(7分)
由(Ⅰ)得 . (8分)
. (8分)
由圆心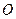 在
在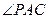 的内部,可知
的内部,可知
 .
.因为
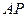 与⊙O相切于点
与⊙O相切于点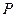 ,所以
,所以 . (1分)
. (1分)因为
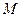 是⊙O的弦
是⊙O的弦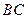 的中点,所以
的中点,所以 . (2分)
. (2分)于是
 . (3分)
. (3分)由圆心
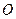 在
在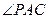 的内部,可知四边形
的内部,可知四边形 的对角互补,所以
的对角互补,所以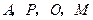 四点共圆.(5分)
四点共圆.(5分)(Ⅱ)解:由(Ⅰ)得
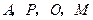 四点共圆,所以
四点共圆,所以 .(7分)
.(7分)由(Ⅰ)得
 . (8分)
. (8分)由圆心
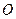 在
在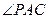 的内部,可知
的内部,可知
略

练习册系列答案
相关题目
 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 .
. 与(1)中所求点
与(1)中所求点 是坐标原点,且
是坐标原点,且 ,求△
,求△ 的面积的取值范围.
的面积的取值范围.
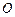 外一点
外一点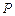 作圆
作圆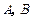 ,
,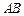 与
与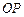 交于点
交于点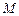 ,设
,设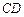 为过点
为过点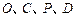 四点共圆.
四点共圆.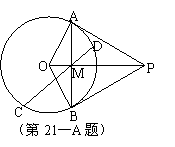
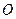 中,
中,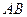 为直径,
为直径,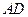 为 弦,过
为 弦,过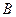 点的切线与
点的切线与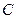 ,且
,且
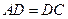 ,则
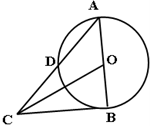
,则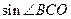 =_________
=_________
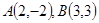 为直径端点作圆,所作圆与
为直径端点作圆,所作圆与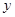 轴有交点
轴有交点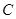 ,则交点
,则交点



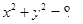 上动点,B(2,0),O为原点,那么
上动点,B(2,0),O为原点,那么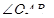 的最大值为
的最大值为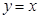 上一点
上一点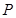 引圆
引圆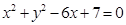 的切线,则切线长的最小值为
的切线,则切线长的最小值为



 轴上,且与直线
轴上,且与直线 相切于点
相切于点 的圆的方程为____ ________________
的圆的方程为____ ________________ AB于D点,则CD= 。
AB于D点,则CD= 。