题目内容
(2012•西城区二模)曲线C是平面内到定点F(0,1)和定直线l:y=-1的距离之和等于4的点的轨迹,给出下列三个结论:
①曲线C关于y轴对称;
②若点P(x,y)在曲线C上,则|y|≤2;
③若点P在曲线C上,则1≤|PF|≤4.
其中,所有正确结论的序号是
①曲线C关于y轴对称;
②若点P(x,y)在曲线C上,则|y|≤2;
③若点P在曲线C上,则1≤|PF|≤4.
其中,所有正确结论的序号是
①②③
①②③
.分析:设出曲线上的点的坐标,求出曲线方程,画出图象,即可判断选项的正误.
解答:解:设P(x,y)是曲线C上的任意一点,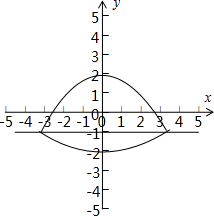
因为曲线C是平面内到定点F(0,1)和定直线l:y=-1的距离之和等于4的点的轨迹,
所以|PF|+|y+1|=4.即
+|y+1|=4,
解得y≥-1时,y=2-
x2,当y<-1时,y=
x2-2;
显然①曲线C关于y轴对称;正确.
②若点P(x,y)在曲线C上,则|y|≤2;正确.
③若点P在曲线C上,|PF|+|y+1|=4,|y|≤2,则1≤|PF|≤4.正确.
故答案为:①②③.
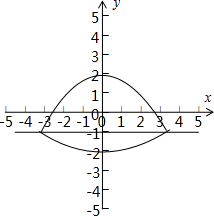
因为曲线C是平面内到定点F(0,1)和定直线l:y=-1的距离之和等于4的点的轨迹,
所以|PF|+|y+1|=4.即
| x2+(y-1)2 |
解得y≥-1时,y=2-
| 1 |
| 4 |
| 1 |
| 12 |
显然①曲线C关于y轴对称;正确.
②若点P(x,y)在曲线C上,则|y|≤2;正确.
③若点P在曲线C上,|PF|+|y+1|=4,|y|≤2,则1≤|PF|≤4.正确.
故答案为:①②③.
点评:本题考查曲线轨迹方程的求法,曲线的基本性质的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•西城区二模)如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.
(2012•西城区二模)如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB. (2012•西城区二模)执行如图所示的程序框图,若输入如下四个函数:
(2012•西城区二模)执行如图所示的程序框图,若输入如下四个函数: