题目内容
15、学校餐厅每天供应1000名学生用餐,每星期一有A、B两样菜可供选择,调查资料表明,凡是在这星期一选A菜的,下星期一会有20%改选B;而选B菜的,下星期一则有30%改选A,若用An,Bn表示在第n个星期一分别选A、B的人数.
(1)试用An,Bn,表示An+1.
(2)证明An+1=0.5An+300.
(3)若A1=a,则An=(0.5)n-1(a-600)+600 (n≥1).
(1)试用An,Bn,表示An+1.
(2)证明An+1=0.5An+300.
(3)若A1=a,则An=(0.5)n-1(a-600)+600 (n≥1).
分析:(1)根据“凡是在这星期一选A菜的,下星期一会有20%改选B;而选B菜的,下星期一则有30%改选A”,可得 An+1=0.8An+0.3Bn;
(2) 由学校餐厅每天供应1000名学生用餐,得到Bn=1000-An代入 An+1=0.8An+0.3Bn,可证;
(3)根据(2)的结果,根据An+1=0.5An+300,两边同时加同一个常数,构造一个等比数列,求通项公式,即可求得结果.
(2) 由学校餐厅每天供应1000名学生用餐,得到Bn=1000-An代入 An+1=0.8An+0.3Bn,可证;
(3)根据(2)的结果,根据An+1=0.5An+300,两边同时加同一个常数,构造一个等比数列,求通项公式,即可求得结果.
解答:解:(1)∵凡是在这星期一选A菜的,下星期一会有20%改选B;而选B菜的,下星期一则有30%改选A,若用An,Bn表示在第n个星期一分别选A、B的人数,
得 An+1=0.8An+0.3Bn ①
(2)∵学校餐厅每天供应1000名学生用餐,
∴Bn+An=1000,即Bn=1000-An并代入①,
得An+1=0.5An+300. ②
(3) 设An+1+λ=0.5(An+λ),即An+1=0.5An-0.5λ,得-0.5λ=300,∴λ=-600.
∴{An-600}是以A1-600=a-600为首项,公比为0.5的等比数列.
∴An-600=(a-600)×0.5n-1.
∴An=600+(a-600)×0.5n-1
得 An+1=0.8An+0.3Bn ①
(2)∵学校餐厅每天供应1000名学生用餐,
∴Bn+An=1000,即Bn=1000-An并代入①,
得An+1=0.5An+300. ②
(3) 设An+1+λ=0.5(An+λ),即An+1=0.5An-0.5λ,得-0.5λ=300,∴λ=-600.
∴{An-600}是以A1-600=a-600为首项,公比为0.5的等比数列.
∴An-600=(a-600)×0.5n-1.
∴An=600+(a-600)×0.5n-1
点评:此题是个中档题.考查根据实际问题抽象数列模型的能力,并能根据模型的解决,指导实际生活中的决策问题,考查学生的阅读能力和分析解决问题的能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
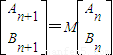 ,请你写出二阶矩阵M;
,请你写出二阶矩阵M;