题目内容
 如图,已知直线l与抛物线y=
如图,已知直线l与抛物线y=| 1 |
| 4 |
(1)若动点M满足
| AB |
| BM |
| 2 |
| AM |
(2)若过点B的直线l'(斜率不等于零)与(1)中的轨迹C交于不同
的两点E、F(E在B、F之间),且
| BE |
| BF |
分析:(1)由y=
x2,知y′=
x,所以l的斜率为y'x=2=1,从而得到直线l的方程为y=x-1,点A坐标为A(1,0),由此能求出动点M的轨迹C的方程.
(2)由题意,设l'的方程为y=k(x-2)(k≠0),由
,得(2k2+1)x2-8k2x+8k2-2=0.由△>0得0<k2<
.设E(x1,y1),F(x2,y2),再结合韦达定理进行求解.
| 1 |
| 4 |
| 1 |
| 2 |
(2)由题意,设l'的方程为y=k(x-2)(k≠0),由
|
| 1 |
| 2 |
解答:解:(1)∵y=
x2,∴y′=
x,
∴l的斜率为y'x=2=1
∴直线l的方程为y=x-1
∴点A坐标为A(1,0)
设M(x、y),
则
=(1,0),
=(x-2,y),
=(x-1,y)
由
•
+
|
|=0得x-2+
•
=0
整理得
+y2=1--------(6分)
(2)由题意,设l'的方程为y=k(x-2)(k≠0)
由
得(2k2+1)x2-8k2x+8k2-2=0由△>0得0<k2<
设E(x1,y1),F(x2,y2),
则
①
∵
=λ
,
∴x1-2=λ(x2-2)②
且0<λ<1
由①知,(x1-2)+(x2-2)=
③
(x1-2)(x2-2)=x1x2-2(x1+x2)+4=
④
由②③④知:
∴
=
即k2=
-
∵0<k2<
,
∴0<
-
<
解得 3-2
<λ<3+2
又0<λ<1
∴3-2
<λ<1--------------(14分)
| 1 |
| 4 |
| 1 |
| 2 |
∴l的斜率为y'x=2=1
∴直线l的方程为y=x-1
∴点A坐标为A(1,0)
设M(x、y),
则
| AB |
| BM |
| AM |
由
| AB |
| BM |
| 2 |
| AM |
| 2 |
| (x-1)2+y2 |
整理得
| x2 |
| 2 |
(2)由题意,设l'的方程为y=k(x-2)(k≠0)
由
|
得(2k2+1)x2-8k2x+8k2-2=0由△>0得0<k2<
| 1 |
| 2 |
设E(x1,y1),F(x2,y2),
则
|
∵
| BE |
| BF |
∴x1-2=λ(x2-2)②
且0<λ<1
由①知,(x1-2)+(x2-2)=
| -4 |
| 2k2+1 |
(x1-2)(x2-2)=x1x2-2(x1+x2)+4=
| 2 |
| 2k2+1 |
由②③④知:
∴
| λ |
| (1+λ)2 |
| 2k2+1 |
| 8 |
即k2=
| 4λ |
| (1+λ)2 |
| 1 |
| 2 |
∵0<k2<
| 1 |
| 2 |
∴0<
| 4λ |
| (1+λ)2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得 3-2
| 2 |
| 2 |
又0<λ<1
∴3-2
| 2 |
点评:本题考查动点的轨迹的求解方法和求λ的取值范围.解题时要认真审题,注意抛物线性质的灵活运用和韦达定理的合理运用.

练习册系列答案
相关题目
 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).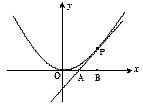 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).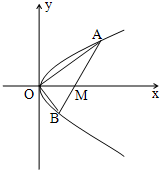 如图,已知直线l与抛物线y2=x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-1,
如图,已知直线l与抛物线y2=x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-1,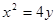 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0). 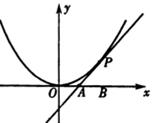
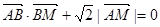 ,求点M的轨迹C;
,求点M的轨迹C;