题目内容
 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).(1)若动点M满足
| AB |
| BM |
| 2 |
| AM |
(2) F1,F2是轨迹Q的左、右焦点,过F1作直线l(不与x轴重合),l与轨迹Q相交于C,D,并与圆x2+y2=3相交于E,F.当
| F2E |
| F2F |
| 2 |
| 3 |
分析:(1)由题意直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,利用导数的几何含义得到直线的方程,进而求出点A的坐标,利用动点M满足
•
+
|
|=0,利用求动点轨迹的直接法即可求解;
(2)由题意设出直线l的方程,把它与椭圆及已知的圆的方程方程进行联立,利用根与系数的关系整体代换得到△F2CD的面积用t表示的函数式子,有已知的λ的范围得到t的范围,利用求函数值域的方法得到三角形的面积的取值范围.
| AB |
| BM |
| 2 |
| AM |
(2)由题意设出直线l的方程,把它与椭圆及已知的圆的方程方程进行联立,利用根与系数的关系整体代换得到△F2CD的面积用t表示的函数式子,有已知的λ的范围得到t的范围,利用求函数值域的方法得到三角形的面积的取值范围.
解答:解:(1)由x2=4y得y=
x2,∴y′=
x
∴直线l的斜率为y′|2=1,
故l的方程为y=x-1,∴点A坐标为(1,0),
设M(x,y)则
=(1,0),
=(x-2,y),
=(x-1,y),
由
•
+
|
|=0得
(x-2)+y•0+
•
=0
整理,得
+y2=1,
∴动点M的轨迹Q为以原点为中心,焦点在x轴上,长轴长为2
,
短轴长为2的椭圆.
(2)设l方程为x=ty-1,E(x1,y1),F(x2,y2)
由
得(t2+1)y2-2ty-2=0
•
=(x1-1,y1)•(x2-1,y2)
=(ty1-2)(ty2-2)+y1y2
=(t2+1)y1y2-2t(y1+y2)+4
=
-2,
由
•
∈[
,1]得t2∈[
,
].
由
得(t2+2)y2-2ty-1=0设C(x3,y3),D(x4,y4).
则S△F1CD=
|F1F2|y3-y4|=|y3-y4|=
,
设m=t2+1,则S=
=
,m∈[
,
]
S关于m在[
,
]上是减函数.所以S∈[
,
].
| 1 |
| 4 |
| 1 |
| 2 |
∴直线l的斜率为y′|2=1,
故l的方程为y=x-1,∴点A坐标为(1,0),
设M(x,y)则
| AB |
| BM |
| AM |
由
| AB |
| BM |
| 2 |
| AM |
(x-2)+y•0+
| 2 |
| (x-1)2+y2 |
整理,得
| x2 |
| 2 |
∴动点M的轨迹Q为以原点为中心,焦点在x轴上,长轴长为2
| 2 |
短轴长为2的椭圆.
(2)设l方程为x=ty-1,E(x1,y1),F(x2,y2)
由
|
| F2E |
| F2F |
=(ty1-2)(ty2-2)+y1y2
=(t2+1)y1y2-2t(y1+y2)+4
=
| 4 |
| t2+1 |
由
| F2E |
| F2F |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
由
|
则S△F1CD=
| 1 |
| 2 |
|
设m=t2+1,则S=
|
|
| 4 |
| 3 |
| 3 |
| 2 |
S关于m在[
| 4 |
| 3 |
| 3 |
| 2 |
| 4 |
| 5 |
| 3 |
| 4 |
| 7 |
| 6 |
点评:此题考查了导数的几何含义,双曲线的性质,直线方程与椭圆和圆的方程的联立及根与系数的关系,还考查了有定义域求函数值域的方法,及整体代换的思想.

练习册系列答案
相关题目
 如图,已知直线l与抛物线
如图,已知直线l与抛物线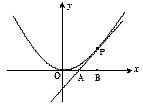 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).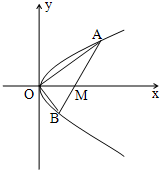 如图,已知直线l与抛物线y2=x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-1,
如图,已知直线l与抛物线y2=x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-1,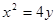 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0). 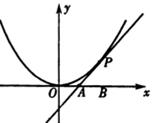
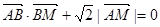 ,求点M的轨迹C;
,求点M的轨迹C;