题目内容
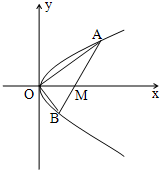 如图,已知直线l与抛物线y2=x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-1,
如图,已知直线l与抛物线y2=x相交于A(x1,y1),B(x2,y2)两点,与x轴相交于点M,若y1y2=-1,(1)求证:OA⊥OB;
(2)M点的坐标为(1,0),求△AOB的面积的最小值.
分析:(1 ) 设M点的坐标为(x0,0),直线l方程为 x=my+x0,代入y2=x得y2-my-x0=0 可证得M点的坐标为(1,0).再根据y1y2=-1结合向量的坐标运算得出OA⊥OB.
(2)直线AB过点(1,0),OA⊥OB,当直线AB过(1,0)且垂直于x轴时,△AOB的面积的取最小值.由此能求出结果.
(2)直线AB过点(1,0),OA⊥OB,当直线AB过(1,0)且垂直于x轴时,△AOB的面积的取最小值.由此能求出结果.
解答:解:(1 ) 设M点的坐标为(x0,0),直线l方程为 x=my+x0,代入y2=x得
y2-my-x0=0 ①,
y1、y2是此方程的两根,
∴x0=-y1y2=1,即M点的坐标为(1,0).
∵y1y2=-1
∴x1x2+y1y2=y12y22+y1y2=y1y2(y1y2+1)=0,
∴OA⊥OB.
(2)由方程①,y1+y2=m,y1y2=-1,且|OM|=x0=1,
于是S△AOB=
|OM||y1-y2|=
=
≥1,
∴当m=0时,△AOB的面积取最小值1.
y2-my-x0=0 ①,
y1、y2是此方程的两根,
∴x0=-y1y2=1,即M点的坐标为(1,0).
∵y1y2=-1
∴x1x2+y1y2=y12y22+y1y2=y1y2(y1y2+1)=0,
∴OA⊥OB.
(2)由方程①,y1+y2=m,y1y2=-1,且|OM|=x0=1,
于是S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| (y1+y2)2-4y1y2 |
| 1 |
| 2 |
| m2+4 |
∴当m=0时,△AOB的面积取最小值1.
点评:本题考查抛物线的简单性质,考查三角形面积的最小值的求法,解题时要认真审题,仔细解答,注意抛物线性质的合理运用.

练习册系列答案
相关题目
 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0). 如图,已知直线l与抛物线
如图,已知直线l与抛物线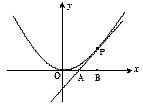 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).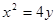 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0). 
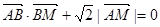 ,求点M的轨迹C;
,求点M的轨迹C;