题目内容
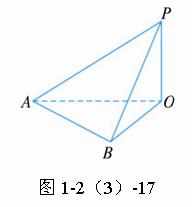
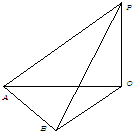地面上有一旗杆OP，如图，为了测得它的高度，在地面上选一基线AB，测得AB=20m，在A处测得点P的仰角为30°，在B处测得点P的仰角为45°，同时可测得∠AOB=30°，求旗杆的高度．
解：设旗杆的高度为hm．依题意，可得PO⊥OA，PO⊥OB，
∴OB=OP=h（m），
（m）
由余弦定理，可得AB2=OA2+OB2-2OA•OBcos∠AOB
即400=3h2+h2-3h2，解得h=20（m）
∴旗杆的高度为20m．
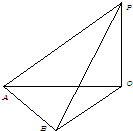
分析：设旗杆的高度为hm．依题意，可得PO⊥OA，PO⊥OB，由题意可得，OB=OP=h（m），，结合余弦定理，可得AB2=OA2+OB2-2OA•OBcos∠AOB可求h
点评：本题主要考查了三角函数及余弦定理在解实际问题中的三角形中的应用，解题的关键是要把实际问题转化为数学中的三角形问题，属于解三角形在实际中的应用．
∴OB=OP=h（m），
（m）由余弦定理，可得AB2=OA2+OB2-2OA•OBcos∠AOB
即400=3h2+h2-3h2，解得h=20（m）
∴旗杆的高度为20m．
分析：设旗杆的高度为hm．依题意，可得PO⊥OA，PO⊥OB，由题意可得，OB=OP=h（m），
，结合余弦定理，可得AB2=OA2+OB2-2OA•OBcos∠AOB可求h点评：本题主要考查了三角函数及余弦定理在解实际问题中的三角形中的应用，解题的关键是要把实际问题转化为数学中的三角形问题，属于解三角形在实际中的应用．
练习册系列答案
相关题目
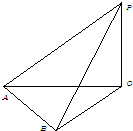地面上有一旗杆OP，如图，为了测得它的高度，在地面上选一基线AB，测得AB=20m，在A处测得点P的仰角为30°，在B处测得点P的仰角为45°，同时可测得∠AOB=30°，求旗杆的高度．
