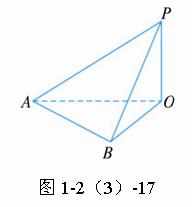
题目内容
地面上有一旗杆OP,如图1-2(3)-17,为了测得它的高度,在地面上选一基线AB,测得AB=

思路分析:设旗杆的高度为h,由题意知∠OAP=30°,∠OBP=45°,旗杆OP垂直于地面,即△AOP和△BOP都是直角三角形,在△AOB中,可利用余弦定理构造方程求解.
解:设旗杆的高度为h,由题意知∠OAP=30°,∠OBP=45°.
在Rt△AOP中,OA=OPcot30°=![]() h,
h,
在Rt△BOP中,OA=OBcot45°=h.
在△AOB中,由余弦定理,得
AB2=OA2+OB2-2OA·OBcos60°,
即202=(![]() h)2+h2-23h×h×
h)2+h2-23h×h×![]() .
.
∴h2=![]() ≈176.4.
≈176.4.
∴h≈13.
∴旗杆的高度为

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
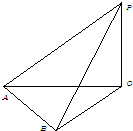 地面上有一旗杆OP,如图,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=30°,求旗杆的高度.
地面上有一旗杆OP,如图,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=30°,求旗杆的高度.
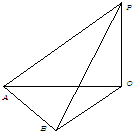 地面上有一旗杆OP,如图,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=30°,求旗杆的高度.
地面上有一旗杆OP,如图,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=30°,求旗杆的高度.