题目内容
已知等比数列 中,
中, ,前
,前 项和是前
项和是前 项中所有偶数项和的
项中所有偶数项和的 倍.
倍.
(1)求通项 ;
;
(2)已知 满足
满足 ,若
,若 是递增数列,求实数
是递增数列,求实数 的取值范围.
的取值范围.
(1)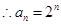 (2)
(2)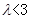
解析试题分析:(1)由前 项和是前
项和是前 项中所有偶数项和的
项中所有偶数项和的 倍可求出公比q的值,再根据等比数列的通项公式和
倍可求出公比q的值,再根据等比数列的通项公式和 ,求出a1的值,即得到通项
,求出a1的值,即得到通项 .
.
(2)首先求出bn的表达式,然后根据 是递增数列,列出关于
是递增数列,列出关于 的不等式,分离出
的不等式,分离出 即可求解.
即可求解.
(1)由已知得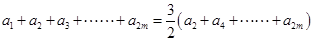
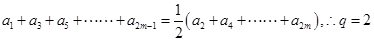
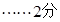
又由 得
得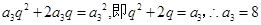
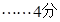
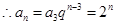
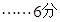
(2)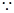
 是递增数列,
是递增数列,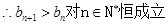
且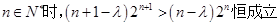
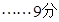
得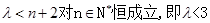
考点: 1.等比数列的性质;2.不等式恒成立问题.

练习册系列答案
相关题目
(2011•山东)等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且其中的任何两个数不在下表的同一列.
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
(2)若数列{bn}满足:bn=an+(﹣1)nlnan,求数列{bn}的前2n项和S2n.
 的左、右顶点分别是
的左、右顶点分别是 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 .若
.若 ,
, ,
, 成等比数列,求此椭圆的离心率.
成等比数列,求此椭圆的离心率. 中,
中, ,前
,前 项的和是
项的和是 ,且
,且 ,
, .
.
 .
. ,从甲容器中取出
,从甲容器中取出 溶液,将其倒入乙容器中搅匀,再从乙容器中取出
溶液,将其倒入乙容器中搅匀,再从乙容器中取出 ,
, ,第
,第 次调和后的甲、乙两种溶液的浓度分别记为:
次调和后的甲、乙两种溶液的浓度分别记为: 、
、 .
. 分别表示
分别表示 ;
; .
. }的前n项和为
}的前n项和为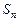 ,且
,且 .
.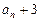 }为等比数列
}为等比数列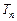
 中,
中, 若
若 ,则
,则 = .
= . ,3
,3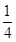 ,5
,5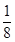 ,7
,7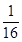 ,…
,…