题目内容
数列 中,
中, ,前
,前 项的和是
项的和是 ,且
,且 ,
, .
.
(1)求出 
(2)求数列 的通项公式;
的通项公式;
(3)求证: .
.
(1)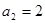 ,
,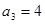 ,
,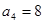 (2)
(2)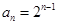 (3)见解析.
(3)见解析.
解析试题分析:(1)利用数列递推式,代入计算,可求a2,a3,a4;(2)再写一式,两式相减,即可求数列{an}的通项公式;(3)求出前n项和,代入计算,可以证得结论.
(1)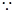
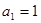 ,
, ∴当
∴当 时,
时,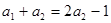 ,
, ∴
∴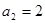 ;
;
当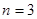 时,
时, ,∴
,∴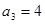 , 当
, 当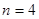 时,
时,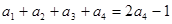 ,∴
,∴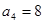
(2)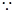
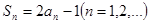 (1) , ∴
(1) , ∴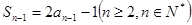 (2)
(2)
(1)-(2)得 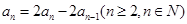 , 即
, 即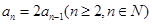 ,
,
所以数列 是以1为首项,2为公比的等比数列,
是以1为首项,2为公比的等比数列,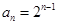 ;
;
(3)证明: 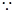
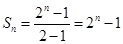 ,∴
,∴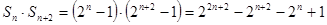
 , ∴
, ∴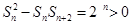 , ∴
, ∴ .
.
考点:数列与不等式的综合;等比关系的确定.

练习册系列答案
相关题目
某地今年年初有居民住房面积为 m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
m2,其中需要拆除的旧房面积占了一半,当地有关部门决定每年以当年年初住房面积的10%的住房增长率建设新住房,同时每年拆除xm2的旧住房,又知该地区人口年增长率为4.9‰.
(1)如果10年后该地区的人均住房面积正好比目前翻一番,那么每年应拆除的旧住房面积x是多少?
(2)依照(1)拆房速度,共需多少年能拆除所有需要拆除的旧房?
下列数据供计算时参考:
| 1.19=2.38 | 1.00499=1.04 |
| 1.110=2.6 | 1.004910=1.05 |
| 1.111=2.85 | 1.004911=1.06 |
 中,已知
中,已知 ,则该数列的前12项的和为 .
,则该数列的前12项的和为 . ,
,  满足条件:
满足条件:
 ,
,  .
. 是等比数列,并求数列
是等比数列,并求数列 项和
项和 ,并求使得
,并求使得 对任意
对任意 N*都成立的正整数
N*都成立的正整数 的最小值.
的最小值. 的前
的前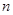 项和为
项和为 ,且
,且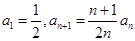 .
.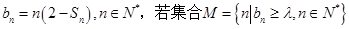 恰有5个元素,求实数
恰有5个元素,求实数 的取值范围.
的取值范围. 中,
中, ,前
,前 项和是前
项和是前 项中所有偶数项和的
项中所有偶数项和的 倍.
倍. ;
; 满足
满足 ,若
,若 的取值范围.
的取值范围. 的前
的前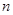 项和为
项和为 ,已知
,已知 成等差数列,(1)求数列
成等差数列,(1)求数列 ,(2)若
,(2)若 ,求
,求 的前
的前 项和为
项和为 ,
, .
. log2an+1 ,求数列
log2an+1 ,求数列 的前
的前 。
。