题目内容
(200
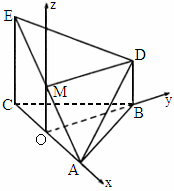
6北京宣武模拟)如下图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD.(1)
求异面直线DA与BC所成的角;(2)
求证:平面DAE⊥平面CEA;(3)
求面EDA与面ABC所成二面角的大小.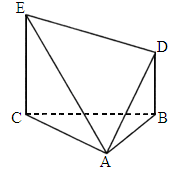
答案:略
解析:
解析:
|
解析: (1)取EA中点M,连结DM.以AC中点O为原点,OA所在直线为x轴,OB所在直线为y轴,OM所在直线为z轴,建立空间直角坐标系.
设 BD=a,则A(a,0,0),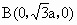 ,C(-a,0,0),E(-a,0,2a),M(0,0,a), ,C(-a,0,0),E(-a,0,2a),M(0,0,a),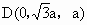 . .
∴异面直线 DA与BC所成的角为 . .
又 CE∩CA=C,∴DM⊥平面ECA,
(3) 由 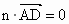 , ,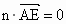 得 得
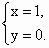
∵ EC⊥平面ABC,∴平面ABC的一个法向量为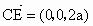 . .
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(2006
北京宣武模拟)设 是由正数组成的等比数列,且
是由正数组成的等比数列,且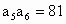 ,那么
,那么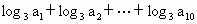 的值是
的值是
[
]|
A .30 |
B .20 |
C .10 |
D .5 |
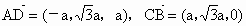
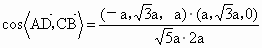
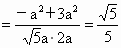
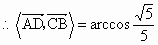
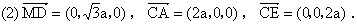
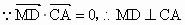
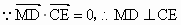
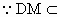
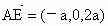

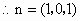
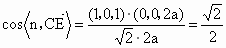
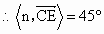
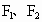 分别是双曲线
分别是双曲线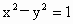 的两个焦点,O为坐标原点,圆O是以
的两个焦点,O为坐标原点,圆O是以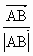 在向量
在向量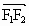 方向的投影是p,当
方向的投影是p,当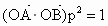 时,求直线l的方程;
时,求直线l的方程;
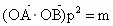 ,且满足2≤m≤4时,求△AOB面积的取值范围(其中p为(2)中所述).
,且满足2≤m≤4时,求△AOB面积的取值范围(其中p为(2)中所述).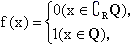 则
则
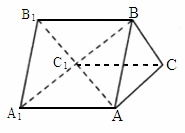
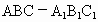 是所有棱长均为a的正三棱柱,则点
是所有棱长均为a的正三棱柱,则点 到平面
到平面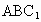 的距离为________.
的距离为________.