题目内容
(2006
北京宣武模拟)已知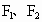 分别是双曲线
分别是双曲线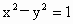 的两个焦点,O为坐标原点,圆O是以
的两个焦点,O为坐标原点,圆O是以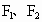 为直径的圆,直线l∶y=kx+b与圆O相切,并与双曲线交于A、B两点.
为直径的圆,直线l∶y=kx+b与圆O相切,并与双曲线交于A、B两点.
(1)
根据条件求出b和k满足的关系式;(2)
向量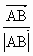 在向量
在向量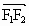 方向的投影是p,当
方向的投影是p,当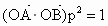 时,求直线l的方程;
时,求直线l的方程;
(3)
当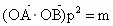 ,且满足2≤m≤4时,求△AOB面积的取值范围(其中p为(2)中所述).
,且满足2≤m≤4时,求△AOB面积的取值范围(其中p为(2)中所述).
答案:略
解析:
解析:
|
解析: (1)双曲线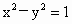 的两上焦点分别是 的两上焦点分别是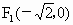 , ,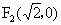 ,从而圆O的方程为 ,从而圆O的方程为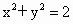 .由于直线y=kx+b与圆O相切,所以有 .由于直线y=kx+b与圆O相切,所以有 . .
即 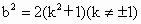 为所求. 为所求.
(2) 设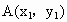 、 、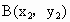 ,则由 ,则由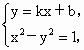 消去y并整理,得 消去y并整理,得
其中  . .
根据韦达定理,得
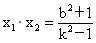 . .
从而 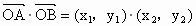 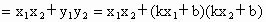
又由 (1)知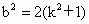 , ,
∴ 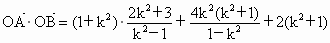 . .
又由于 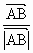 在 在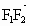 方向上的投影为p, 方向上的投影为p,
所以 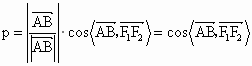 . .
∴ 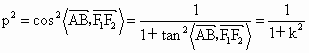 . .
∴ 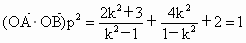 . .
即 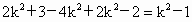 , ,
∴ 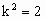 ,∴ ,∴ ,∴ ,∴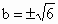 ,此时方程(*)满足Δ>0. ,此时方程(*)满足Δ>0.
所以直线 l的方程为
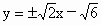 . .
(3) 由(2)得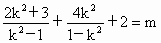 , ,
即 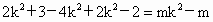 . .
∴  , , . .
根据弦长公式,得
而 2≤m≤4,此时方程(*)满足Δ>0.
∴△ AOB面积的取值范围是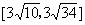 . . |

练习册系列答案
相关题目
(2006
北京宣武模拟)设 是由正数组成的等比数列,且
是由正数组成的等比数列,且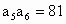 ,那么
,那么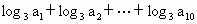 的值是
的值是
[
]|
A .30 |
B .20 |
C .10 |
D .5 |
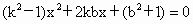
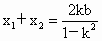
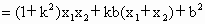
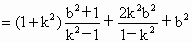
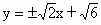
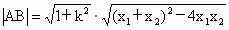
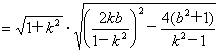
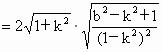
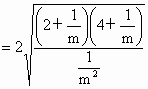
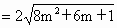
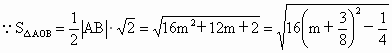
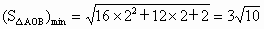
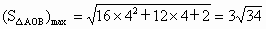
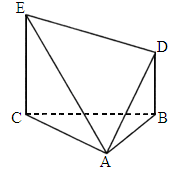
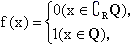 则
则
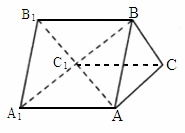
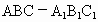 是所有棱长均为a的正三棱柱,则点
是所有棱长均为a的正三棱柱,则点 到平面
到平面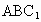 的距离为________.
的距离为________.