题目内容
12.已知函数f(x)=|ex-1|+1,若a<b,f(a)=f(b),则实数a+b的取值范围为( )| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,1] | D. | (0,1) |
分析 先画出函数f(x)=|ex-1|+1的图象,数形结合得到满足条件的a,b满足ea+eb=2,结合指数的运算性质和基本不等式,可得答案.
解答 解:函数f(x)=|ex-1|+1的图象如下图所示: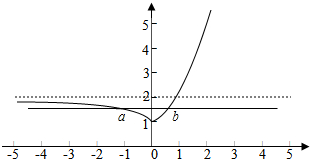
由图可得:若a<b,f(a)=f(b),
则-(ea-1)+1=(eb-1)+1,
即ea+eb=2>2ea+b,
即ea+b<1,
即a+b<0,
故实数a+b的取值范围为(-∞,0),
故选:A.
点评 本题考查的知识点是指数函数的单调性的应用,基本不等式,是函数与不等式的综合应用,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知在(x-2)8的展开式中,x的指数为正偶数的所有项的系数和为( )
| A. | 3281 | B. | -3281 | C. | -3025 | D. | 3025 |
2.设函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则f(a)的值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |