题目内容
数列{an} 的各项均为正数,a1=p,p>0,k∈N*,an+an+k=f(p,k)•pn.
(1)当k=1,f(p,k)=p+k,p=5时,求a2,a3;
(2)若数列{an}成等比数列,请写出f(p,k)满足的一个条件,并写出相应的通项公式(不必证明);
(3)当k=1,f(p,k)=p+k时,设Tn=a1+2a2+3a3+…+2an+an+1,求Tn.
解:(1)由题意,an+an+1=6•5n,
∵a1=p=5,
∴a2=25,a3=125
(2)数列{an}成等比数列,设公比为q,则an=p×qn-1,
∴an+k=p×qn+k-1,
∴an+an+k=p×qn-1+p×qn+k-1=(1+qk)×p×qn-1,
∵an+an+k=f(p,k)•pn
∴q=p时,f(p,k)=1+pk时,an+an+k=(1+pk)•pn且an=pn.
(3)当k=1,f(p,k)=p+k时,an+an+1=(1+p)pn.
由(2)知,∴Tn=a1+2a2+3a3+…+2an+an+1=(a1+a2)+(a2+a3)+…+(an+an+1)=(1+p)(p+p2+…+pn)
p=1时,Tn=2n;当p≠1且p>0时,Tn=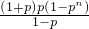 .
.
分析:(1)由题意,an+an+1=6•5n,利用a1=p=5,代入计算,即可求得a2,a3;
(2)设出公比,利用an+an+k=f(p,k)•pn,即可得到当f(p,k)=1+pk时,an=pn.
(3)当k=1,f(p,k)=p+k时,an+an+1=(1+p)pn,再利用分组求和,即可得到结论.
点评:本题考查数列递推式,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.
∵a1=p=5,
∴a2=25,a3=125
(2)数列{an}成等比数列,设公比为q,则an=p×qn-1,
∴an+k=p×qn+k-1,
∴an+an+k=p×qn-1+p×qn+k-1=(1+qk)×p×qn-1,
∵an+an+k=f(p,k)•pn
∴q=p时,f(p,k)=1+pk时,an+an+k=(1+pk)•pn且an=pn.
(3)当k=1,f(p,k)=p+k时,an+an+1=(1+p)pn.
由(2)知,∴Tn=a1+2a2+3a3+…+2an+an+1=(a1+a2)+(a2+a3)+…+(an+an+1)=(1+p)(p+p2+…+pn)
p=1时,Tn=2n;当p≠1且p>0时,Tn=
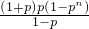 .
.分析:(1)由题意,an+an+1=6•5n,利用a1=p=5,代入计算,即可求得a2,a3;
(2)设出公比,利用an+an+k=f(p,k)•pn,即可得到当f(p,k)=1+pk时,an=pn.
(3)当k=1,f(p,k)=p+k时,an+an+1=(1+p)pn,再利用分组求和,即可得到结论.
点评:本题考查数列递推式,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )