题目内容
已知圆与y轴相切,圆心在直线x-3y=0,且这个圆经过点A(6,1),求该圆的方程.
(x-3)2+(y-1)2=9或(x-111)2+(y-37)2=1112
试题分析:因为圆心在x-3y=0上,所以设圆心坐标为(3m,m)且m>0,
根据圆与y轴相切得到半径为3m,
所以,圆的方程为(x-3m)2+(y-m)2=9m2,把A(6,1)代入圆的方程得:(6-3m)2+(1-m)2=9m2,
化简得:m2-38m+37=0,则m=1或37,
所以,圆的方程为(x-3)2+(y-1)2=9或(x-111)2+(y-37)2=1112。
点评:中档题,用待定系数法求圆的方程,一般可通过已知条件,设出所求方程,再建立待定系数的方程组求解。

练习册系列答案
相关题目
 是以
是以 为直径的半圆
为直径的半圆 上的一点,过
上的一点,过 ,交过A点的切线于
,交过A点的切线于 ,
, .
.
 是圆
是圆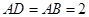 ,求
,求 .
. 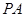 是
是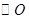 的切线,
的切线,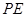 过圆心
过圆心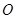 ,
, 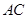 为
为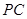 与
与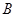 、
、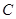 两点,连结
两点,连结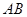 、
、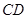 . (1) 求证:
. (1) 求证: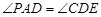 ;
;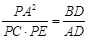 .
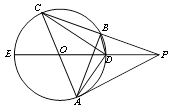
.
 被圆
被圆 截得的弦长为( )
截得的弦长为( )
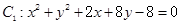 与圆
与圆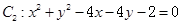 相交,则圆
相交,则圆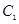 与圆
与圆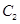 的公共弦所在的直线的方程是
的公共弦所在的直线的方程是  的切线,则切线长为( )
的切线,则切线长为( )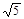
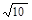
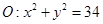 ,椭圆
,椭圆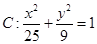 .
.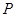 在圆
在圆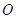 上,线段
上,线段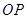 的垂直平分线经过椭圆的右焦点,求点
的垂直平分线经过椭圆的右焦点,求点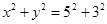 上任意一点
上任意一点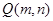 作椭圆
作椭圆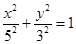 的两条切线,则这两条切线互相垂直”;
的两条切线,则这两条切线互相垂直”;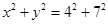 上任意一点
上任意一点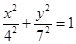 的两条切线,则这两条切线互相垂直”.
的两条切线,则这两条切线互相垂直”. 和
和 分别是圆
分别是圆 的切线, 且
的切线, 且 ,
, ,延长
,延长 到
到 点,则△
点,则△ 的面积是___________.
的面积是___________.