设平面向量$\overrightarrow{a}$=(1.2).$\overrightarrow{b}$=.若$\overrightarrow{a}$⊥$\overrightarrow{b}$.则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=5．题目和参考答案——青夏教育精英家教网——

题目内容

17．设平面向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，y），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=5．

分析由向量垂直的条件：数量积为0，可得y=1，再由向量的模的公式和向量的模的平方即为向量的平方，计算即可得到．

解答解：平面向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，y），
若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则$\overrightarrow{a}$•$\overrightarrow{b}$=0，
即有-2+2y=0，
解得y=1，
即有|$\overrightarrow{a}$|=$\sqrt{5}$，|$\overrightarrow{b}$|=$\sqrt{5}$，
则|2$\overrightarrow{a}$-$\overrightarrow{b}$|²=（2$\overrightarrow{a}$-$\overrightarrow{b}$）²=4${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$
=4×5-4×0+5=25，
则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=5．
故答案为：5．

点评本题考查向量的数量积的坐标表示和性质，主要考查向量的平方即为模的平方，以及向量垂直的条件，属于基础题．

练习册系列答案

同步拓展与训练系列答案

升级创优卷系列答案

一课3练三好练习系列答案

金版卷王名师面对面期末大冲刺系列答案

大阅读周周练系列答案

高分拔尖提优教程系列答案

培优闯关NO1期末冲刺卷系列答案

全解全习课时达标讲练测系列答案

完全大考卷冲刺名校系列答案

实验探究与指导系列答案

相关题目

1．已知x，y，z，a∈R，且x²+4y²+z²=6，则使不等式x+2y+3z≤a恒成立的a的最小值为（　　）

8．设复数z₁，z₂在复平面内的对应点关于虚轴对称，z₁=2+i，则$|{\frac{z_2}{z_1}}|$=1．

5．已知函数f（x）=e^x
（Ⅰ）当f（x）≥ex+a对任意的实数x恒成立，求a的取值范围；
（Ⅱ）若a＜b，a，b∈R，求证：$\frac{f（b）-f（a）}{b-a}$＜$\frac{1}{2}$[$\frac{f（a）+f（b）}{2}$+f（$\frac{a+b}{2}$）]．

12．设函数f（x）=a（x+1）²ln（x+1）+bx（x＞-1），曲线y=f（x）过点（e-1，e²-e+1），且在点（0，0）处的切线方程为y=0．
（Ⅰ）求a，b的值；
（Ⅱ）证明：当x≥0时，f（x）≥x²；
（Ⅲ）若当x≥0时，f（x）≥mx²恒成立，求实数m的取值范围．

2．已知数列{a_n}满足（a_n+1-1）（a_n-1）=3（a_n-a_n+1），a₁=2，令${b_n}=\frac{1}{{{a_n}-1}}$．
（Ⅰ）证明：数列{b_n}是等差数列；
（Ⅱ）求数列{a_n}的通项公式．

9．函数f（x）=Asin（ωx+φ），（0＜φ＜$\frac{π}{2}$）的部分图象如图所示，则（　　）

A=2，φ=$\frac{π}{4}$

A=2，φ=$\frac{π}{6}$

A=2$\sqrt{2}$，φ=$\frac{π}{3}$

A=2$\sqrt{2}$，φ=$\frac{π}{6}$

6．过点P（-2，2）作直线l，使直线l与两坐标轴在第二象限内围成的三角形面积为8，这样的直线l一共有（　　）

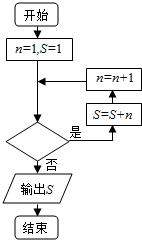已知数列{a_n}中，a₁=1，a_n+1=a_n+n，若利用如图所示的程序框图计算该数列的第10项的值S，则判断框内的条件是n≤9或n＜10．