题目内容
 如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5
如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5| 7 |
(1)求椭圆E的标准方程;
(2)设椭圆E的上顶点为M,直线l交椭圆于P、Q两点,那么是否存在直线l,使B点恰为△PQM的垂心?如果存在,求出直线l的方程;如果不存在,请说明理由.
分析:(1)设椭圆的标准方程为
+
=1,由梯形ABCD的面积是5
可求点C的坐标为(2,
)由2a=|AC|+|CB|=
+
=6
可求2a,2c,进而可求椭圆的方程
(2)解:假设存在直线l与椭圆E相交于P(x1,y1)、Q(x2,y2)两点,且B点恰为△PQM垂心.由KMB=-1,可得KPQ=1,故设直线l的方程为y=x+m
联立
得3x2+4mx+2m2-18=0由
•
=0可得x1(x2-3)+y2(y1-3)=0,从而可求m的值
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| 7 |
(2+3)2+(
|
(2-3)2+
|
| 2 |
(2)解:假设存在直线l与椭圆E相交于P(x1,y1)、Q(x2,y2)两点,且B点恰为△PQM垂心.由KMB=-1,可得KPQ=1,故设直线l的方程为y=x+m
联立
|
| MP |
| BQ |
解答:解:(1)设椭圆的标准方程为
+
=1
在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5
∴
(6+4)•yC=5
,即yC=
,所以点C的坐标为(2,
),
又A(-3,0)、B(3,0)
∴2a=|AC|+|CB|=
+
=6
2c=|AB|=6∴a=3
,c=3,∴b=3
∴椭圆的标准方程为
+
=1
(2)解:假设存在直线l与椭圆E相交于P(x1,y1)、Q(x2,y2)两点,且B点恰为△PQM垂心.
∵M(0,3),B(3,0),
∴KMB=-1,∴KPQ=1,故设直线l的方程为y=x+m
由
得3x2+4mx+2m2-18=0
△=16m2-4×3(2m2-18)>0
∴-3
<m<3
∴x1+x2=-
,x1x2=
∵
•
=0
∴x1(x2-3)+y2(y1-3)=0
故m2+m-12=0
∴m=-4或3,经检验,m=3不合题意,舍去
∴存在直线l:y=x-4,使得B点恰为△PQM的垂心
| x2 |
| a2 |
| y2 |
| b2 |
在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5
| 7 |
∴
| 1 |
| 2 |
| 7 |
| 7 |
| 7 |
又A(-3,0)、B(3,0)
∴2a=|AC|+|CB|=
(2+3)2+(
|
(2-3)2+
|
| 2 |
2c=|AB|=6∴a=3
| 2 |
∴椭圆的标准方程为
| x2 |
| 18 |
| y2 |
| 9 |
(2)解:假设存在直线l与椭圆E相交于P(x1,y1)、Q(x2,y2)两点,且B点恰为△PQM垂心.
∵M(0,3),B(3,0),
∴KMB=-1,∴KPQ=1,故设直线l的方程为y=x+m
由
|
△=16m2-4×3(2m2-18)>0
∴-3
| 3 |
| 3 |
∴x1+x2=-
| 4m |
| 3 |
| 2m2-18 |
| 3 |
∵
| MP |
| BQ |
∴x1(x2-3)+y2(y1-3)=0
|
故m2+m-12=0
∴m=-4或3,经检验,m=3不合题意,舍去
∴存在直线l:y=x-4,使得B点恰为△PQM的垂心
点评:本题主要考查了利用椭圆的定义求解椭圆的方程及直线与椭圆的位置关系的处理,常见的处理方法是联立方程,根据方程的性质求解,属于综合性试题.

练习册系列答案
相关题目
 如图,在等腰梯形ABCD中,AB∥DC,AB=4,CD=2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO=2,EA∥PO.
如图,在等腰梯形ABCD中,AB∥DC,AB=4,CD=2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO=2,EA∥PO.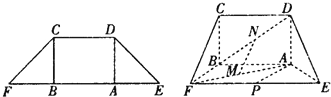 如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2
如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2 选修4-1;几何证明选讲.
选修4-1;几何证明选讲. (2012•河北模拟)如图,在等腰梯形ABCD中,CD=2,AB=4,AD=BC=
(2012•河北模拟)如图,在等腰梯形ABCD中,CD=2,AB=4,AD=BC=