题目内容
如图，在△ABC中，B=45°，D是BC边上的一点，AD=5，AC=7，DC=3，则AB的长为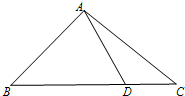
分析：先根据余弦定理求出∠ADC的值，即可得到∠ADB的值，最后根据正弦定理可得答案．
解答：解：在△ADC中，AD=5，AC=7，DC=3，
由余弦定理得cos∠ADC=
=-
，
∴∠ADC=120°，∠ADB=60°
在△ABD中，AD=5，∠B=45°，∠ADB=60°，
由正弦定理得
=
，
∴AB=
故答案为：
．
由余弦定理得cos∠ADC=
| AD2+DC2-AC2 |
| 2AD•DC |
| 1 |
| 2 |
∴∠ADC=120°，∠ADB=60°
在△ABD中，AD=5，∠B=45°，∠ADB=60°，
由正弦定理得
| AB |
| sin∠ADB |
| AD |
| sinB |
∴AB=
5
| ||
| 2 |
故答案为：
5
| ||
| 2 |
点评：本题主要考查余弦定理和正弦定理的应用，在解决问题的过程中要灵活运用正弦定理和余弦定理．属基础题．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知