题目内容
判定下列命题的真假
(1)两个平面垂直,过其中一个平面内一点作与它们的交线垂直的直线,必垂直于另一个平面;
(2)两个平面垂直,分别在这两个平面内且互相垂直的两直线,一定分别与另一平面垂直;
(3)两平面垂直,分别在这两个平面内的两直线互相垂直。
解析:
(1)若该点在两个平面的交线上,则命题是错误的,
如图2-55,正方体AC1中,平面AC⊥平面AD1,平面AC∩平面AD1=AD,
 在AD上取点A,连结AB1,则AB1⊥AD,即过棱上一点A的直线AB1
在AD上取点A,连结AB1,则AB1⊥AD,即过棱上一点A的直线AB1
与棱垂直,但AB1与平面ABCD不垂直,其错误的原因是AB1没有保证在平面ADD1A1内,可以看出:线在面内这一条件的重要性;
(2)该命题注意了直线在平面内,但不能保证这两条直线都与棱垂直,如图2-56,在正方体AC1中,平面AD1⊥平面AC,AD1![]() 平面ADD1A1,AB
平面ADD1A1,AB![]() 平面ABCD,且AB⊥AD1,即AB与AD1相互垂直,但AD1与平面ABCD不垂直;
平面ABCD,且AB⊥AD1,即AB与AD1相互垂直,但AD1与平面ABCD不垂直;
(3)如图2-56:正方体AC1中,平面ADD1A1⊥平面ABCD,AD1![]() 平面ADD1A1,AC
平面ADD1A1,AC![]() 平面ABCD,AD1与AC所成的角为60,即AD1与AC不垂直
平面ABCD,AD1与AC所成的角为60,即AD1与AC不垂直
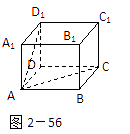 由上面的分析知,命题⑴、⑵、⑶都是假命题。
由上面的分析知,命题⑴、⑵、⑶都是假命题。
点评:在利用两个平面垂直的性质定理时,要注意下列的三个条件缺一不可:①两个平面垂直;②直线必须在其中一个面内;③直线必须垂直它们的交线。

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
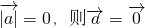 ;
;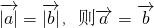 ;
;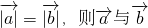 是平行向量.
是平行向量.