题目内容
已知集合M={直线的倾斜角},集合N={两条异面直线所成的角},集合P={直线与平面所成的角},则下面结论中正确的个数为( )
①M∩N∩P=(0,
]
②M∪N∪P=[0,π]
③(M∩N)∪P=[0,
]
④(M∪N)∩P=(0,
).
①M∩N∩P=(0,
| π |
| 2 |
②M∪N∪P=[0,π]
③(M∩N)∪P=[0,
| π |
| 2 |
④(M∪N)∩P=(0,
| π |
| 2 |
分析:根据直线的倾斜角、异面直线所成的角、空间直线与平面所成的角的定义求出集合M、N、P,再进行集合运算.
解答:解:∵根据定义,M=[0,π),N=(0,
],P=[0,
]
∴M∩N∩P=(0,
],①正确;
M∪N∪P=[0,π),②不正确;
(M∩N)∪P=[0,
],∴③正确;
(M∪N)∩P=[0,
],∴④不正确.
故选C
| π |
| 2 |
| π |
| 2 |
∴M∩N∩P=(0,
| π |
| 2 |
M∪N∪P=[0,π),②不正确;
(M∩N)∪P=[0,
| π |
| 2 |
(M∪N)∩P=[0,
| π |
| 2 |
故选C
点评:本题借助考查集合的混合运算,考查直线的倾斜角、异面直线所成的角、空间直线与平面所成的角的范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
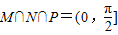
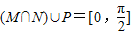
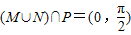 .
.