题目内容
已知集合M={直线的倾斜角},集合N={两条异面直线所成的角},集合P={直线与平面所成的角},则(M∩N)∪P=分析:首先分别对集合M,N,P进行分析,求出取值范围,然后根据集合交并补集的运算进行计算即可.
解答:解:∵集合M={直线的倾斜角}
而直线倾斜角的取值范围为:[0,π)
∴M=[0,π)
∵集合N={两条异面直线所成的角},
而两条异面直线所成角的范围为:(0,
]
∵集合P={直线与平面所成的角},
而直线与平面所成的角范围:[0,
]
∴(M∩N)∪P=(0,
]
故答案为:(0,
].
而直线倾斜角的取值范围为:[0,π)
∴M=[0,π)
∵集合N={两条异面直线所成的角},
而两条异面直线所成角的范围为:(0,
| π |
| 2 |
∵集合P={直线与平面所成的角},
而直线与平面所成的角范围:[0,
| π |
| 2 |
∴(M∩N)∪P=(0,
| π |
| 2 |
故答案为:(0,
| π |
| 2 |
点评:本题考查交并补集的运算,涉及到直线的倾斜角,两条一面直线所成的角,直线与平面所成的角的取值范围问题,属于基础题.

练习册系列答案
相关题目
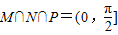
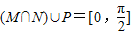
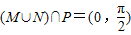 .
.