题目内容
设集合A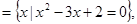 B
B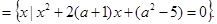
(1)若A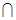 B
B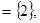 求实数a的值;
求实数a的值;
(2)若A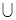 B=A求实数a的取值范围;
B=A求实数a的取值范围;
【答案】
(1)-1或-3. (2)a≤-3.
【解析】
试题分析:由x2-3x+2=0得x=1或x=2,故集合A=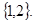
(1)∵A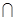 B
B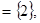 ∴2
∴2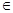 B,代入B中的方程,得a2+4a+3=0,∴a=-1或a="-3;"
B,代入B中的方程,得a2+4a+3=0,∴a=-1或a="-3;"
当a=-1时,B=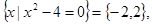 满足条件;
满足条件;
当a=-3时,B= 满足条件;
满足条件;
综上,a的值为-1或-3.
(2)对于集合B,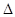 =4(a+1)2-4(a2-5)=8(a+3).
=4(a+1)2-4(a2-5)=8(a+3).
∵A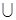 B=A∴B
B=A∴B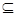 A,
A,
①当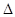 <0,即a<-3时,B=
<0,即a<-3时,B=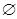 ,满足条件;
,满足条件;
②当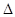 =0,即a=-3时,B=
=0,即a=-3时,B=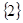 ,满足条件;
,满足条件;
③当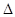 >0,即a>-3时,B=A=
>0,即a>-3时,B=A=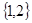 才能满足条件, 则由根与系数的关系得
才能满足条件, 则由根与系数的关系得
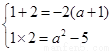 即
即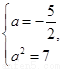 矛盾;综上,a的取值范围是a≤-3.
矛盾;综上,a的取值范围是a≤-3.
考点:本题考查了集合的关系及运算
点评:对于比较抽象的集合,在探究它们的关系时,要先对它们进行化简。同时,要注意集合的子集要考虑空与不空,不要忘了集合本身和空集这两种特殊情况.

练习册系列答案
相关题目
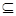 B,则a的范围是
B,则a的范围是