题目内容
设集合A![]() B
B![]()
(1)若A![]() B
B![]() 求实数a的值;
求实数a的值;
(2)若A![]() B=A求实数a的取值范围;
B=A求实数a的取值范围;
(3)若U=R,A![]() (
(![]() UB)=A.求实数a的取值范围.
UB)=A.求实数a的取值范围.
(1) a的值为-1或-3 (2) a≤-3 (3)a的取值范围是a<-3或-3<a<-1-![]() 或-1-
或-1-![]() <a<-1或-1<a<-1+
<a<-1或-1<a<-1+![]() 或a>-1+
或a>-1+![]()
解析:
由x2-3x+2=0得x=1或x=2,故集合A=![]() 2分
2分
(1)∵A![]() B
B![]() ∴2
∴2![]() B,代入B中的方程,得a2+4a+3=0,∴a=-1或a=-3;
B,代入B中的方程,得a2+4a+3=0,∴a=-1或a=-3;
当a=-1时,B=![]() 满足条件;
满足条件;
当a=-3时,B=![]() 满足条件;
满足条件;
综上,a的值为-1或-3. 4分
(2)对于集合B,![]() =4(a+1)2-4(a2-5)=8(a+3).
=4(a+1)2-4(a2-5)=8(a+3).
∵A![]() B=A∴B
B=A∴B![]() A,
A,
①当![]() <0,即a<-3时,B=
<0,即a<-3时,B=![]() ,满足条件;
,满足条件;
②当![]() =0,即a=-3时,B=
=0,即a=-3时,B=![]() ,满足条件;
,满足条件;
③当![]() >0,即a>-3时,B=A=
>0,即a>-3时,B=A=![]() 才能满足条件, 6分
才能满足条件, 6分
则由根与系数的关系得
![]() 即
即![]() 矛盾;
矛盾;
综上,a的取值范围是a≤-3. 9分
(3)∵A![]() (
(![]() UB)=A,∴A
UB)=A,∴A![]()
![]() UB,∴A
UB,∴A![]() B=
B=![]() ; 10分
; 10分
①若B=![]() ,则
,则![]() <0
<0![]() 适合;
适合;
②若B≠![]() ,则a=-3时,B=
,则a=-3时,B=![]() ,A
,A![]() B=
B=![]() ,不合题意;
,不合题意;
a>-3,此时需1![]() B且2
B且2![]() B.将2代入B的方程得a=-1或a=-3(舍去);
B.将2代入B的方程得a=-1或a=-3(舍去);
将1代入B的方程得a2+2a-2=0![]()
∴a≠-1且a≠-3且a≠-1![]() 13分
13分
综上,a的取值范围是a<-3或-3<a<-1-![]() 或-1-
或-1-![]() <a<-1或-1<a<-1+
<a<-1或-1<a<-1+![]() 或a>-1+
或a>-1+![]() 14分
14分

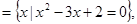 B
B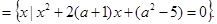
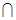 B
B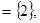 求实数a的值;
求实数a的值;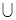 B=A求实数a的取值范围;
B=A求实数a的取值范围;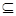 B,则a的范围是
B,则a的范围是