题目内容
(本小题满分14分)已知数列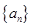 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为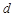 ,
, 为其前
为其前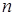 项和,且满足
项和,且满足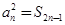 ,
,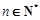 .数列
.数列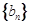 满足
满足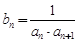 ,
,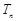 为数列
为数列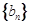 的前
的前 项和.
项和.
(1)求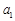 、
、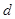 和
和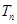 ;
;
(2)若对任意的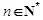 ,不等式
,不等式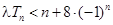 恒成立,求实数
恒成立,求实数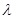 的取值范围;
的取值范围;
(3)是否存在正整数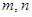
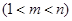 ,使得
,使得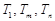 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有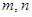 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) ,
, ,
,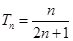 .
.
(2)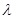 的取值范围是
的取值范围是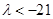 .
.
(3)当且仅当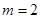 ,
, 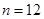 时,数列
时,数列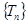 中的
中的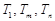 成等比数列.
成等比数列.
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设等差数列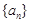 的公差d不为0,
的公差d不为0,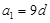 ,若
,若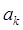 是
是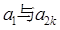 的等比中项,则k=( )
的等比中项,则k=( )
| A.2 | B.6 | C.8 | D.4 |
已知等差数列{an}的前n项和为Sn,S4=40,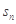 =210,
=210,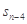 =130,则n=( ).
=130,则n=( ).
| A.12 | B.14 | C.16 | D.18 |
设 是等差数列
是等差数列 的前
的前 项和,
项和,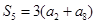 , 则
, 则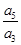 的值为( ).
的值为( ).
A. | B.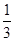 | C.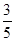 | D. |
等差数列 的前
的前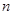 项和为
项和为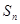 ,若
,若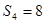 ,
,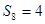 ,则
,则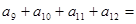 ( )
( )
A.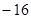 | B.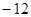 | C.12 | D.16 |
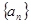 的前
的前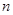 项和
项和 ,则
,则 ________________;
________________;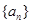 的前
的前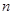 项和为
项和为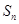 ,且
,且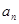 是
是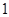 的等差中项,等差数列
的等差中项,等差数列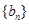 满足
满足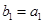 ,
,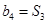 .
.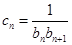 ,数列
,数列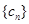 的前
的前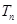 ,证明:
,证明: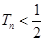 .
.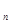 }满足0<a
}满足0<a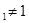 , 且
, 且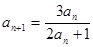 (n
(n N*).
N*). 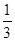 ,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.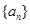 是首项为2,公比为
是首项为2,公比为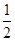 的等比数列,数列
的等比数列,数列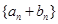 是首项为-2,第三项为2的等差数列.
是首项为-2,第三项为2的等差数列.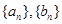 的通项式.
的通项式.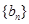 的前
的前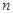 项和
项和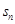 .
.