题目内容
18.已知点P在曲线y=x2+1上,若曲线y=x2+1在点P处的切线与曲线y=-2x2-1相切,求点P的坐标.分析 先设P(x0,y0),根据导数的几何意义求出函数f(x)在x=x0处的导数,从而求出切线的斜率,再用点斜式写出方程,根据此直线与曲线y=-2x2-1相切,转化成方程2x2+2x0x+2-x02=0只有一解,然后利用判别式为0,进行求解即可.
解答 解:设P(x0,y0),y=x2+1的导数为y′=2x,
由题意知曲线y=x2+1在P点的切线斜率为k=2x0,
则切线方程为y=2x0x+1-x02,
而此直线与曲线y=-2x2-1相切,
∴切线与曲线只有一个交点,
即方程2x2+2x0x+2-x02=0的判别式△=4x02-2×4×(2-x02)=0.
解得x0=±$\frac{2}{3}$$\sqrt{3}$,y0=$\frac{7}{3}$.
∴P点的坐标为($\frac{2}{3}$$\sqrt{3}$,$\frac{7}{3}$)或(-$\frac{2}{3}$$\sqrt{3}$,$\frac{7}{3}$).
点评 本题考查利用导数求曲线上过某点切线方程的斜率,以及直线与二次函数相切的条件,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知曲线C1:$\frac{{x}^{2}}{8-k}$-$\frac{{y}^{2}}{4}$=1与C2:$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{6-k}$=1都是双曲线,则( )
| A. | 0<k<8,C1与C2的实轴长相等 | B. | k<6,C1与C2的实轴长相等 | ||
| C. | 0<k<8,C1与C2的焦距相等 | D. | k<6,C1与C2的焦距相等 |
3.过定点A(0,a)在x轴上截得弦长为2a的动圆圆心的轨迹方程是( )
| A. | x2+(y-a)2=a2 | B. | y2=2ax | C. | (x-a)2+y2=a2 | D. | x2=2ay |
7.已知函数f(x)=$\frac{{e}^{x}}{|x|}$,关于x的方程f2(x)+(m+1)f(x)+m+4=0(m∈R)有四个相异的实数根,则m的取值范围是( )
| A. | (-4,-e-$\frac{4}{e+1}$) | B. | (-4,-3) | C. | (-e-$\frac{4}{e+1}$,-3) | D. | (-e-$\frac{4}{e+1}$,+∞) |
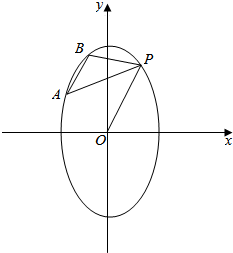 点P在椭圆3x2+y2=12上,OP倾斜角为60°,AB∥OP,A,B在椭圆上且都在x轴上方,求△ABP面积的最大值及此时直线AB的方程.
点P在椭圆3x2+y2=12上,OP倾斜角为60°,AB∥OP,A,B在椭圆上且都在x轴上方,求△ABP面积的最大值及此时直线AB的方程.