题目内容
10.定义在R上的函数f(x)在[8,+∞)上为减函数,且函数y=f(x+8)为奇函数,则f(x)的图象关于(8,0)对称,且f(x)在(-∞,8)上为减函数(填增、减).分析 根据函数奇偶性的性质,结合奇函数的单调性的性质进行判断即可.
解答 解:∵函数y=f(x+8)为奇函数,
∴f(x+8)关于原点对称,即f(x)关于(8,0)对称,
∵函数f(x)在[8,+∞)上为减函数,
∴函数f(x)在(-∞,8)上为减函数
故答案为:(8,0),减
点评 本题主要考查函数奇偶性和单调性的应用,要求熟练掌握函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.如图所示是一个几何体的三视图,则这个几何体外接球的表面积是( )
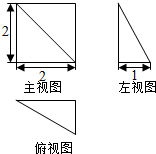

| A. | 16π | B. | 9π | C. | 12π | D. | 36π |
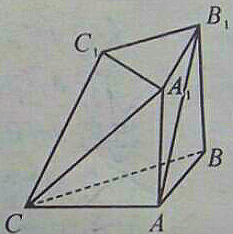 如图在多面体ABC-A1B1C1中,AA1$\underset{∥}{=}$BB1,B1C1$\underset{∥}{=}$$\frac{1}{2}$BC,求证:AB1∥平面 A1C1C.
如图在多面体ABC-A1B1C1中,AA1$\underset{∥}{=}$BB1,B1C1$\underset{∥}{=}$$\frac{1}{2}$BC,求证:AB1∥平面 A1C1C.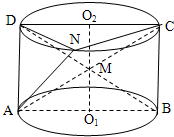 如图,已知矩形ABCD是圆柱O1O2的轴截面,N在上底面的圆周O2上,AC,BD相交于点M.
如图,已知矩形ABCD是圆柱O1O2的轴截面,N在上底面的圆周O2上,AC,BD相交于点M.